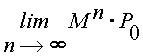
Como hemos visto en las clases anteriores, no siempre existe la distribución asintótica en una cadena de Markov, o de otra forma no siempre existe
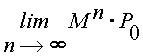
Es claro que mediante la resolución espectral de la potencia de una matriz de Markov, sabremos si existe la distribución "asintótica" o no. No obstante mediante análisis de los estados de una cadena de Markov, podemos encontrar condiciones para la existencia de esta probabilidad.
Sean i y j dos estados de una cadena de Markov, diremos que j es accesible desde i si
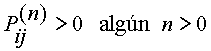
De otra forma el estado j es accesible desde i si existe una probabilidad positiva de que en un número finito de transiciones el estado j puede ser alcanzado desde el estado i. Diremos que los estados i y j son comunicativos si ambos son mutuamente accesibles. Entonces dos estados i y j son no comunicativos si ocurre una o ambas situaciones:
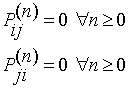
La relación comunicativos es una relación de equivalencia entre los estados, luego esta relación define una partición en el espacio de estados agrupados en clases de equivalencia. Veamos un ejemplo, sea la matriz de transición
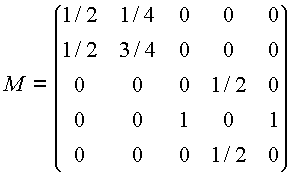
el grafo asociado a esta cadena de Markov es
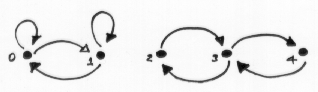
Las clases de equivalencia son {0,1}, {2,3,4}. Si el estado inicial pertenece a la clase del {0,1} entonces, cualquiera sea el tiempo, permanecerá en esa clase, y para cualquier estudio del desarrollo dinámico de este sistema la matriz relevante será
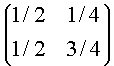
De manera análoga, si el proceso se inicia en los estados {2,3,4}, entonces para cualquier tiempo posterior el proceso seguirá en dicha clase, y la matriz relevante será
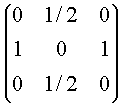
El ejemplo anterior indica que al haber dos clases existe una "reducción" de la matriz de transición que dependerá de cuál es el estado inicial del proceso. Esto nos induce a entregar la siguiente definición. Diremos que una cadena de Markov es irreducible si la relación de equivalencia "comunicativos" genera una única clase. Esto es, el proceso es irreducible si todos los estados son comunicativos.
Veamos dos ejemplos. Consideremos una cadena de Markov con espacio de estado S={0,1,2, ..., a} de modo que su matriz de transición sea
Entonces aquí existen tres clases, a saber {0}, {1,2, ..., a-1} y {a}. Observemos que desde la segunda clase es posible llegar a las clases exteriores, pero toda vez que se entre allí no se puede salir (se dice que los estados {0} y {a} son absorventes). Esta cadena de Markov no es irreducible.
Entregaremos ahora una cadena de Markov irreducible que estará representada por la matriz
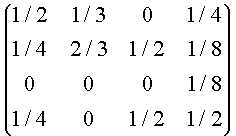
Una manera de ver que todos sus estados son comunicativos es trazar el grafo asociado a este proceso. En efecto
y se ve claramente que existe una única clase.
Periodicidad de una cadena de Markov: Se define el período de un
estado i, y se denota por d(i), como el máximo común divisor
de los enteros 
para los
cuales 
Ahora si 
se
define d(i) = 0. A modo de
ejemplo consideremos el paseo aleatorio de manera que 
(vea la sección 1.2, pag. 6 de los
apuntes de
Cadenas
de Markov, en pdf), entonces es fácil verificar que d(i)
= 2 para cualquier estado i. Ahora si para este paseo aleatorio existe un
estado k tal que 
, entonces cada estado i tiene período d(i) = 1,
puesto que si el estado inicial es i, el sistema puede alcanzar el estado k
y permanecer allí (eventualmente) cualquier longitud de tiempo antes de retornar a i.
Ejemplo: Consideremos una cadena de Markov de n estados y con matriz de transición:
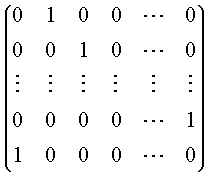
Es fácil convencerse que d(i) = n para todo i = 1, 2,..., n