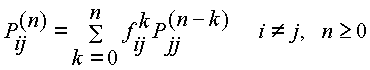Objetivo: Seguiremos estudiando las propiedades de los estados de una cadena de Markov.
Existen tres propiedades básicas del período de un estado que se puede verificar con lápiz y papel para diversas cadenas de Markov
Esta propiedad asegura que el retorno a i puede ocurrir para todo múltiplo de d(i) suficientemente grande.
para todo n suficientemente grande.
Una cadena de Markov en la que cada estado tiene período 1 es llamada aperiódica. Una gran parte de las cadenas de Markov caen dentro de esta clasificación.
Recurrencia. Vamos a definir el "regreso a casa en n pasos por primera vez". Para el estado i y el tiempo n definimos la probabilidad
Esto es, 
es
la probabilidad de que, partiendo desde el estado i, el primer regreso al estado i
ocurra en la n-ésima transición.
Es claro que 
. Ahora la probabilidad 
se puede calcular recursivamente de acuerdo a
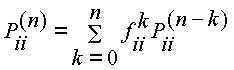
donde se define 
.
De manera similar podemos definir la probabilidad 
; esto es, como la probabilidad
de la primera llegada desde el estado i al estado j en la n-ésima
transición. Se define, además, 
. También es fácil verificar que
