|
La densidad uniforme |
||
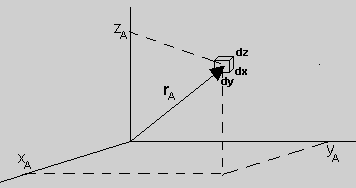
Figura 1 Supongamos que una molécula A está ubicada dentro de un recipiente cúbico de volumen V (=abc, componentes respectivas a lo largo de los ejes cartesianos). Supongamos además que intentamos seguir la trayectoria de esta molécula A mediante un vector rA cuyas componentes sobre los ejes de un sistema cartesiano son XA, YA y ZA. Como la trayectoria de esta molécula es aleatoria, el vector rA y por lo tanto sus componentes también son aleatorias. Supongamos que la molécula lleva una posición dentro del volumen infinitesimal dt = dx dy dz ¿Cuál es la probabilidad de que la flecha del vector rA se encuentre dentro del volumen dt? Como el volumen es infinitamente pequeño, la probabilidad buscada, que llamaremos dW, debe ser proporcional a este volumen, esto es dW = w dt (1) El factor de proporcionalidad w, que dependerá de las coordenadas (x, y, z) (al interior de dt), es llamada la densidad de probabilidad del vector rA. Entonces, el producto de la densidad de probabilidad de un vector aleatorio con el elemento de volumen dt da la probabilidad de que la flecha del vector rA esté dentro del volumen dt o, en otras palabras, que las siguientes condiciones ocurran simultáneamente: las componentes x, y, y z del vector rA estén contenidas en los intervalos x + dx, y + dy, y, z + dz, respectivamente. Por otro lado, en la sección de la probabilidad binomial habíamos visto que la probabilidad de que la molécula A se encuentre en el interior de dt está dada por dW = dt / V (2) De modo que comparando (1) y (2) podemos concluir que w = w(x, y, z) = 1 / V |
|
Si las componentes de un vector aleatorio son independientes, como ocurre con el movimiento espacial de una molécula (alejada de la velocidad de la luz, es decir de la teoría de la relatividad), en este caso, entonces, la densidad de probabilidad w(x, y, z) está representada por el producto de las tres densidades, como intentaremos explicar a continuación: w(x, y, z) es la probabilidad de que la molécula se encuentre en el interior del volumen pequeño dt, y esto significa que las proyecciones en los ejes de la molécula XA, YA y ZA deben estar en los intervalos de longitud infinitesimal dx, dy y dz respectivamente. De manera que si denotamos la probabilidad de que la variable aleatoria XA se encuentre en el intervalo de longitud infinitesimal dx por dWx, entonces esta probabilidad debe ser proporcional a la longitud del intervalo infinitesimal, esto es dWx = wx(x) dx (3) donde wx(x) es el factor de proporción, y solamente lo hacemos depender exclusivamente de x, toda vez que hemos aceptado la hipótesis de que el movimiento proyectado sobre el eje X es independiente de las otras dos restantes proyecciones. Razonando de igual forma con las restantes variables de proyección, tenemos que dWy = wy(y) dy (4) dWz = wz(z) dz (5) De modo que las probabilidades infinitesimales de (3), (4) y (5) determinan la probabilidad de que la posición de la molécula se encuentre en el volumen infinitesimal dt. Y esto nos conduce a que w(x, y, z) dt = wx(x) dx . wy(y) dy . wz(z) dz Puesto que la densidad w(x, y, z) = 1/V, y además V = abc, y dt = dx dy dz, se concluye que wx(x) = 1/a wy(y) = 1/b wz(z) = 1/c Que son las llamadas densidades de probabilidad uniforme en los intervalos [0, a], [0, b] y [0, c] respectivamente. |