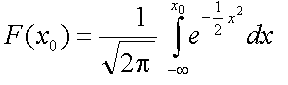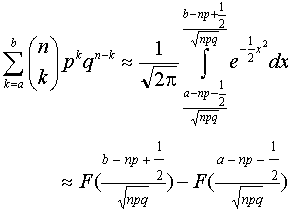|
La densidad normal y la binomial |
||
|
Es uno de los pocos retratos que se tiene, al parecer,
del matemático inglés nacido en Francia. Perteneció a la casta de los
"malditos". En efecto, era hugonote, es decir
protestante, y obviamente fue perseguido por la Francia católica de ese
entonces, que nada tenía que ver con los gritos de libertad, igualdad y
fraternidad, y, obviamente también, fue encarcelado un año en París. No
trabajó jamás en la universidad, y fue muy pobre (con esto no se quiere
decir que los que trabajan en la universidad son necesariamente ricos), y
se ganó la pobreza asesorando a los sindicatos de seguro y apuestas.
Murió ciego, pero más ciego fue el mundo científico, de ese entonces,
que no pudo gozar de sus trabajos intelectuales. En lo que a estos apuntes
interesa, podemos decir que gracias a su trabajo de "aproximación de
la binomial mediante la normal", la mecánica estadística es
bastante accesible y "calculable". Brindemos entonces un
homenaje a este matemático maldito, y utilicemos su famosa aproximación.
Consideremos la función de distribución generada por la densidad normal de parámetros m = 0 y s2 = 1,
|
Entonces, la probabilidad de que un fenómeno aleatorio regido por la ley de probabilidades binomial con parámetros n y p tenga un valor observado que esté entre a y b inclusive, para cualquier entero a y b, se determina aproximadamente por
|
|