|
La probabilidad binomial |
||
|
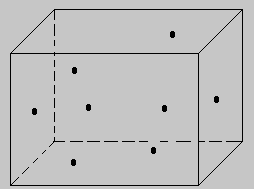
Figura 1 Imagínese un cubo de volumen V, como el que aparece en la figura 1. Suponga que por el interior de ese cubo, hay N moléculas que "vagabundean" erráticas. Suponga que N no es demasiado grande. Si sacamos una fotografía instantánea a ese cubo, tendríamos una situación como lo indica la figura 2.
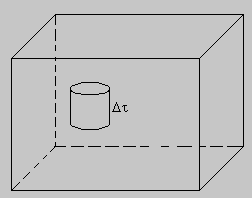
Figura 2 Es importante destacar que el número N de moléculas es pequeño en relación a la capacidad máxima que puede soportar el volumen (*), con el propósito que no exista posibilidad de colisión o interacción entre las moléculas. Ahora fijemos un pequeño volumen en el espacio interior del cubo, que tenga una forma arbitraria, como lo indica la figura 3.
Figura 3 El volumen de la forma interior es Dt Será crucial el hecho de tener pocas moléculas, puesto que con esto estamos diciendo que no hay interacción entre ellas (ni colisiones), de tal forma que las trayectorias y posición de las moléculas serán independientes, si además agregamos que no hay campos magnéticos externos que puedan conducir a una cierta trayectoria en el movimiento de estas moléculas. Con esta condición, vamos a calcular la probabilidad de que una determinada molécula pertenezca a la región espacial S. Parece claro que la probabilidad de que una molécula se encuentre en la región espacial S será proporcional al volumen de la región S esto es si designamos por W a la probabilidad del suceso de que una molécula se encuentre en la región espacial S, se tiene entonces que W = Dt / V |
y la probabilidad de que una molécula no se encuentre en la región espacial S es 1 - W = 1 - Dt / V Supongamos ahora que tomamos una fotografía en un cierto instante de tiempo. Y estamos interesados en saber cuántos moléculas están contenidas en el volumen de la región espacial S en el instante de la fotografía. Es claro que el número de moléculas que podrán aparecer en la fotografía dentro del volumen de S será algún número de entre {0, 1, 2, ..., N}. Denotemos por X el número de moléculas contenida en S. Se dice que X es una variable aleatoria discreta, y tiene asociada una probabilidad que intentaremos descubrir. Para poder deducir esta probabilidad supongamos primero que N = 2. De manera entonces que al tomar la fotografía en el instante dado pueden ocurrir las siguientes cuatro situaciones indicadas en la figura 4
(a) (b) (c) (d) Figura 4 Se puede observar que estos cuatro sucesos son excluyentes. La probabilidad asociada a cada uno de estos eventos, en virtud de la independencia de las trayectorias de las moléculas se entrega a continuación, en términos ahora de la variable aleatoria X, Pr { X = 0 } = (1 - W)2 Pr { X = 1 } = 2 W (1 - W) (**) Pr { X = 2 } = W 2 En general si tenemos ahora N moléculas, entonces podemos deducir que la probabilidad de encontrar k moléculas, con k menor o igual a N, está dada por
(*): Un volumen de un centímetro cúbico, a temperatura y presión normal, contiene la friolera de 2.69*1019 moléculas (**) Note que son los términos del desarrollo de (W + (1 - W)) 2 (***) Es el k-ésimo término del desarrollo de (W + (1 - W)) N
|
|