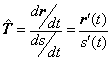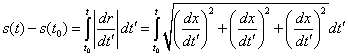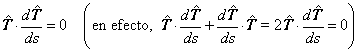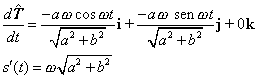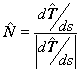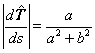| En la sección anterior establecimos que si r( t ) = x( t ) i + y( t ) j + z( t ) k es una curva que eventualmente denote la trayectoria de una partícula y si s = s( t ) describe la longitud de la curva en función de la variable t, entonces |
|
|
| Nota: este resultado se concluye bajo la ecuación (2) de la sección anterior. De tal forma que para calcular el vector tangente a la curva en un punto determinado necesitamos conocer la derivada de la función longitud de curva s( t ), donde esta se obtiene mediante |
|
|
| Y es así, también, que podemos obtener una expresión analítica para la función longitud de arco, integrando esta última ecuación, esto es |
|
|
| Veamos un ejemplo. |
| Consideremos la curva r( t ) = a cos w t i + a sen w t j + bw t k. (a, b y w constantes positivas). la derivada de esta función es |
|
|
| La magnitud o norma de este vector es |
|
|
| De tal forma que el vector tangente a la curva en un punto cualquiera está dado por |
|
|
| Y si queremos medir la longitud de la curva desde 0 hasta el valor de t, tenemos que |
|
|
| Por ejemplo, la longitud de la curva entre los puntos (a, 0, 0) y (a, 0, 2pb), puntos que corresponden a los valores de t = 0 y t = 2p/w respectivamente, es |
|
s( 2p/w ) - s( 0 ) = 2p (a2 + b2)1/2. |
| En particular, si b = 0 obtenemos simplemente el perímetro de la circunferencia de radio a, 2pa, puesto que esta hélice se proyecta como una circunferencia sobre el plano XY. Vea la gráfica. |
| Con este mismo ejemplo, es fácil verificar que efectivamente se cumple (siempre) que |
|
|
| y derivando esta igualdad respecto de la variable longitud de curva s, tenemos que |
|
|
| de modo que aparece otro vector a escena, y que además es ortogonal al vector tangente. ¿Cómo podemos encontrar este nuevo vector? Notemos que |
|
|
| Esta última igualdad se debe al teorema de la función inversa (si no recuerda este teorema haga click en el vínculo). De modo que, en nuestro ejemplo, derivando (1) respecto de t y sabiendo el valor de s'( t ), tenemos que |
|
|
| de manera que, según (3), nos queda |
|
|
| No resulta para nada complicado verificar que efectivamente el vector en (4) es ortogonal al vector tangente en (1). Si ahora hacemos unitario este vector obtenemos un vector unitario ortogonal al vector tangente, que llamaremos vector normal, y se define como |
|
|
| que para nuestro ejemplo |
|
|
| y en consecuencia |
|
|
| Observe la gráfica. Más adelante veremos algunas aplicaciones de este vector normal. |