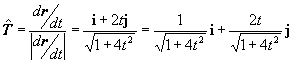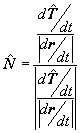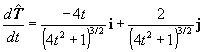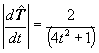| En esta sección vamos a ver en detalle, y a través de un ejemplo sencillo, el cálculo de los vectores tangente y normal a una curva en el plano. |
| Consideremos la gráfica de y = x2. Esta curva se puede llevar a as forma paramétrica de manera trivial. En efecto, consideremos la parábola en su forma paramétrica como |
|
r( t ) = t i + t2 j |
| El cálculo del vector tangente se obtiene por simple derivada respecto de t, y luego se normaliza, esto es |
|
|
| Observemos que el vector tangente es, estrictamente hablando, un vector que es función de t, esto es |
|
|
| El cálculo del vector normal se obtiene mediante |
|
|
| donde |
|
|
| y además |
|
|
| De tal forma que este vector normal es función de t, esto es |
|
|
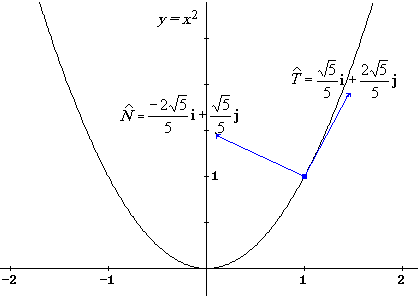
| En particular el punto (1, 1) pertenece a la parábola y su correspondiente valor paramétrico es para t = 1, de modo que |
|
|
| Observemos la gráfica: |
|
|