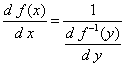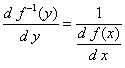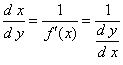| Recordemos el concepto fundamental de función: es una regla en que un número y es obtenido de otro número x. Esta relación usualmente se expresa como |
|
y = f( x ) |
| Sin embargo, una dependencia funcional se puede describir también sin necesidad de resolver la fórmula de dependencia de una variable respecto de la otra, y esta es de la forma |
|
F( x , y) = 0 |
| donde F describe las "operatorias matemáticas" entre x e y de tal forma que el resultado es cero. Por ejemplo |
|
|
| Esta ecuación define implícitamente y como función de x, o viceversa, aún cuando pueden surgir problemas de interpretación en la ambigüedad de los signos, en efecto si despejamos y obtenemos |
|
|
| En este caso, se elige "arbitrariamente" un signo, para que efectivamente sea una función. En cualquier caso se puede obtener la derivada dy / dx de la relación (1). Para esto se deriva cada miembro de la ecuación (1) respecto de x, donde evidentemente la derivada del segundo miembro es cero, esto es |
|
|
| de modo que |
|
|
| luego si hemos decidido en (1) que |
|
|
| la derivada en (2) queda como |
|
|
| Observemos que perfectamente de la relación (1) podemos obtener la derivada dx / dy. Esto es |
|
|
| despejando dx / dy obtenemos |
|
|
| Observemos que de las derivadas en (2) y (3) se concluye que |
|
|
| Esta última relación nos indica que las "diferenciales" dx y dy pueden ser tratadas con el álgebra de los números reales, y la extensión que podemos hacer de (4) es la siguiente, Si y = f( x ) es una función que admite función inversa en un dominio determinado, esto es que existe la función x = f -1( y ), entonces |
|
|
| que es equivalente a |
|
|
| La demostración es bastante sencilla. Tenemos que |
|
|
| derivando implícitamente la última ecuación, nos queda |
|
|
| despejando dx / dy, obtenemos |
|
|
| Ejercicio. Encontrar dy / dx y dx / dy de la relación implícita |
|
|
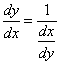 (4)
(4)