| Por simetría el campo vectorial es en
rigor una función del radio de la esfera, esto es |
|
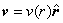
|
donde 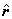 es el vector unitario en la dirección radial. Vamos a
estimar el valor de v( r ) bajo las
hipótesis establecidas para el fluido. El fluido en
cualquier posición del espacio tiene la misma densidad,
de tal forma que no existe acumulación de fluido en
ninguna parte, por lo tanto la rapidez con que sale el
fluido del surtidor debe ser igual a la razón con que
el fluido cruza cualquier esfera concéntrica de radio r.
Supongamos que k es el volumen por unidad de
tiempo con que el fluido sale del surtidor, pues bien
esa cantidad, por conservación de masa, deberá ser
igual a la razón con que el fluido cruza la esfera
concéntrica de radio r, y esta razón es igual a
la velocidad radial que lleva el fluido en la posición r
por el área de la esfera que debe atravesar, esto es
es el vector unitario en la dirección radial. Vamos a
estimar el valor de v( r ) bajo las
hipótesis establecidas para el fluido. El fluido en
cualquier posición del espacio tiene la misma densidad,
de tal forma que no existe acumulación de fluido en
ninguna parte, por lo tanto la rapidez con que sale el
fluido del surtidor debe ser igual a la razón con que
el fluido cruza cualquier esfera concéntrica de radio r.
Supongamos que k es el volumen por unidad de
tiempo con que el fluido sale del surtidor, pues bien
esa cantidad, por conservación de masa, deberá ser
igual a la razón con que el fluido cruza la esfera
concéntrica de radio r, y esta razón es igual a
la velocidad radial que lleva el fluido en la posición r
por el área de la esfera que debe atravesar, esto es |
|
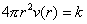
|
| Sin pérdida de generalidad, y
considerando que k es positivo, podemos expresarlo como k
= 4pm, con m
> 0. Nos queda, |
|
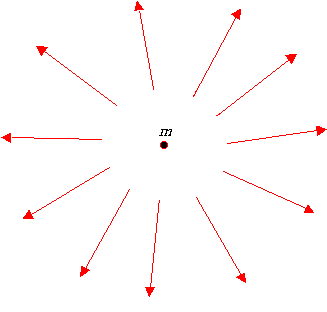
Figura 1 |
|
