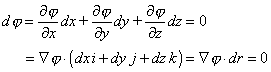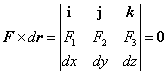Ahora bien, formemos el campo escalar F = Ñj, es decir j es el potencial del campo F. Entenderemos como líneas de flujo (para cualquier campo sea o no conservativo) como la familia de curvas que puede ser construida de tal forma que sus tangentes en cualquier punto sean paralelos al campo vectorial que existe en ducho punto. Observemos la figura 2.

Supongamos entonces que F es el campo vectorial, que será una familia de vectores definidos sobre cada punto de las trayectorias de flujo, entonces si dr es el vector desplazamiento que describe esta trayectoria (para mayor detalle vea estas transparencias) deberá cumplirse que

F x dr = 0

Puesto que F = F₁ i + F₂ j + F₃ k y dr = dx i + dy j + dz k,

Figura 1

entonces

y esto conlleva a que

(1)

Con esto podemos decir para un campo vectorial conservativo F, la líneas de flujo serán perpendiculares a las curvas de nivel del potencial del campo. Veamos un ejemplo.

Figura 2

Ejemplo. Estudiaremos las líneas de flujo y las curvas de nivel del potencial asociado al campo vectorial en dos dimensiones F = x i - y j.

Podemos obtener las líneas de flujo mediante la ecuación (1), esto es

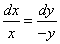
esto nos conduce a que xdy + ydx = d(xy) = 0, lo que al integrar nos da que xy = c, c constante. Y esta ecuación representa a una familia de hipérbolas.

Por otro lado, vamos a encontrar el potencial j de F. En efecto, deberá ocurrir que F = Ñj. De modo que

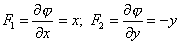
Integrando la primera ecuación

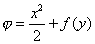
siendo la constante de integración una función de y. Ahora derivamos esta función j respecto de y e igualamos a F₂, y obtenemos

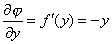
Y ahora integramos,

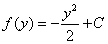
Y se concluye que

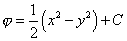
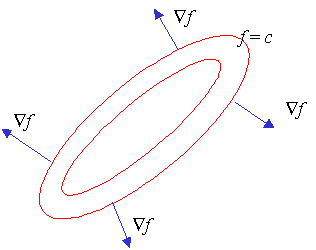
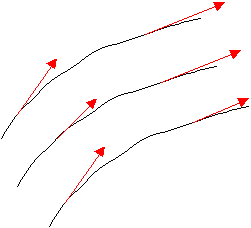
es el potencial del campo F = x i - y j. Y las curvas de nivel de j = cte. serán perpendiculares a xy = cte., como se observa en la Figura 3.

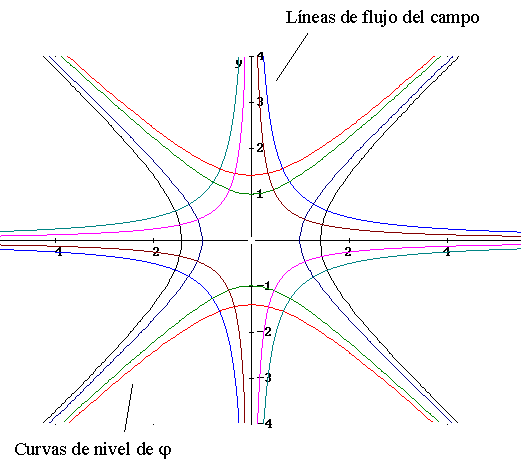
Figura 3

Más sobre campos conservativos