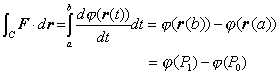| Supongamos que tenemos un campo vectorial F( x, y, z) de tal forma que posee un potencial escalar, esto es F = Ñj. Recuerde que un campo vectorial posee un potencial escalar si rot F = 0, y además la forma de calcular este potencial escalar está dado en la ecuación (12) de esta sección. |
|
Vamos a demostrar que |
|
|
| donde C es una curva seccionalmente suave cuya forma paramétrica está dada por r( t ) con t en [a, b], y está orientada desde P0 = r( a ) hasta P1 = r( b ) . |
| Como F tiene un potencial escalar, entonces |
|
|
| De tal forma que la integral de línea queda como |
|
|
| esto es |
|
|
| Y con esto queda demostrado (1). |
| De este resultado podemos deducir que si F es un campo vectorial que tiene un potencial escalar, entonces la integral |
|
|
| es independiente de la trayectoria C. Y más aún, si la curva es cerrada esto es r( a ) = r( b ), entonces |
|
|
| Nota: el "círculito" en el símbolo de la integral sirve para denotar que se está integrando sobre una curva cerrada. |