Anterior

El teorema de Green: primera versión

La fórmula que estudiaremos se debe a George Green (vea una pequeña biografía pinchando en el nombre, y verá que no es tan terriblemente malo no asistir a clases). Empezaremos por el final. La fórmula esencial del teorema de Green es como sigue:

(1)

Y enseguida intentaremos explicar los diferentes elementos matemáticos involucrados. En primer lugar la relación entre R y C, es como lo indica la Figura 1.

C es una curva cerrada suave, descrita por la forma paramétrica r( t ). Y la región al interior de la curva es precisamente R.

Consideremos el campo vectorial

j ( x, y ) = L( x, y ) i + M( x , y ) j

de modo que esté bien definido en todo punto de R incluida la frontera C, y que sea continuamente diferenciable (esto es que las derivadas parciales no solo existan sino que además sean continuas).

Vamos a ver el significado de la primera integral de (1)

Figura 1

La primera integral es simplemente la integral de línea del campo vectorial j ( x, y ) sobre la curva cerrada C, esto es

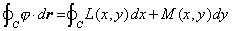
toda vez que j ( x, y ) = L( x, y ) i + M( x , y ) j, y además dr = dx i + dy j.

De modo que lo primero que anuncia el trabajo de Green es que la integral de línea de un campo vectorial sobre una curva cerrada en el plano es igual a una integral doble de una determinada función de dos variables sobre la región contenida al interior de la curva cerrada C.

Nota importante: la orientación de la curva sigue la "regla del tornillo" o de orientación positiva, esto es en el sentido contrario a las manecillas de un reloj antiguo (no sirve reloj digital).

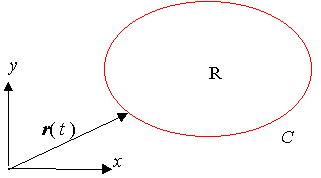
Un aplicación importante de este resultado es el siguiente. Usted sabe que el área de una región R como la de la Figura 1 está dada por la doble integral siguiente

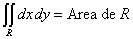(2)

Luego esta integral en comparación con la segunda integral en (1) se consigue cuando L( x, y ) = 0 y M( x , y ) = x, de modo que tenemos un primer resultado

(3)

Donde C es la curva, orientada positivamente, que rodea a la región R. De modo que, si la segunda integral de línea es sencilla, nos permitirá el cálculo de áreas sencillas.

Otra manera de conseguir una expresión para el cálculo del área de una región R como en la figura siguiente es haciendo, conforme a la expresión en (1), L( x, y ) = - y , M( x , y ) = x. De esta forma obtenemos que

(4)

La verdad es que hay divertidas maneras de calcular el área de una región R como la indicada por la Figura 1. En efecto, considere, como antes, que la frontera de R es la curva cerrada C, entonces calculemos la siguiente integral de línea

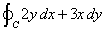
Aplicando la fórmula (1), tenemos que, en este caso, L( x, y ) = 2y, M( x , y ) = 3x, de modo que

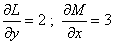
y en consecuencia aplicando el teorema de Green, obtenemos

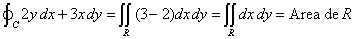
Desde el lado contrario, también puede ser usado. A veces el cálculo de una integral de línea puede ser tedioso, y resulta más sencillo utilizar la integral doble. Veamos el siguiente ejemplo.

Usemos al teorema de Green vara evaluar la integral

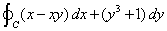
donde C es la frontera del cuadrado con vértices en los puntos (1, 0), (2, 0), (2, 1) y (1, 1), como se muestra en la Figura 2.

Identificamos las funciones componentes como

L( x, y ) = x - xy , M( x , y ) = y³ + 1

De modo que, obtenemos

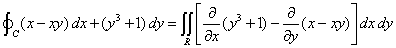
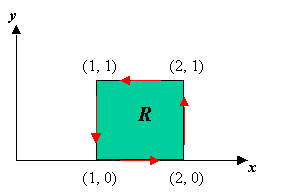
Figura 2

y esta segunda integral doble es sencilla de resolver. En efecto

Esto es