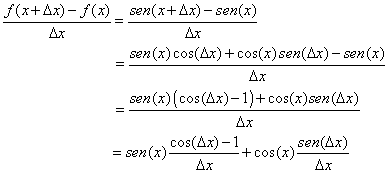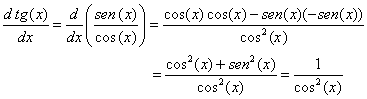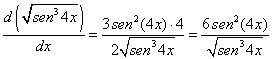| Veremos en esta sección algunas de las derivadas de
funciones más usuales. Empecemos con la función trigonométrica seno. 1.
Sea f ( x ) = sen ( x ) entonces |
|
|
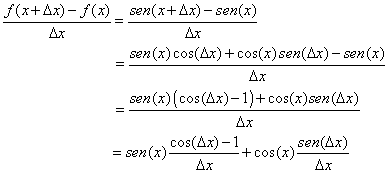
| luego pasando al límite nos queda que |
|
|
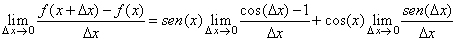
| y puesto que el primer límite del segundo miembro es 0 y
el segundo límite del segundo miembro es 1 (hacer click en cada uno de
los límites para ver la demostración) se concluye que |
|
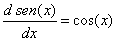(1)
|
| 2. Con la derivada de (1) más la regla de la
cadena podemos calcular rápidamente la derivada de la función coseno.
En efecto, sabemos que |
|
|
|
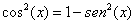
luego derivando ambos miembros de esta igualdad, aplicando (1) y la
regla de la cadena tenemos que |
|
|
|
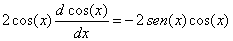
simplificando nos queda que |
|
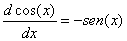(2)
|
|
3. Con las derivadas en (1) y (2) podemos obtener mediante la
regla del cociente la derivada de la tangente, esto es |
|
|
|
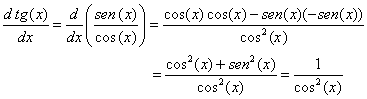
y se tiene que |
|
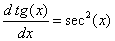(3)
|
|
En definitiva, con estas derivadas puede obtener las derivadas de las
restantes funciones trigonométricas, a saber cotangente, cosecante y
secante puesto que son las inversas de las tres anteriores, y aplicamos
la regla del cociente para las funciones 1 / tg( x ), 1/ sen( x
) y 1 / cos ( x ) respectivamente. |
|
4. Vamos a calcular la derivada del logaritmo natural, ln( x
) aplicando simplemente la definición de logaritmo y la regla de la
cadena. Preste mucha atención: Sea y = ln( x ), esto
significa que |
|
|
|
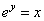
y es a esta igualdad que derivamos respecto de la variable x
(Ojo: y es una función de x, la derivada de x es 1,
y la derivada de la
función
exponencial ya fue calculada), nos queda |
|
|
|
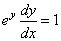
ahora despejamos la derivada dy / dx, y obtenemos
que |
|
|
|
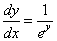
pero como e y = x, tenemos la fórmula |
|
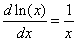(4)
|
|
|
|
Con estas sencillas fórmulas, más las reglas de las derivadas para la
suma, resta, producto y cociente de funciones tenemos herramientas más
que suficiente para realizar el cálculo de derivadas de funciones más
complicadas. |
Ejemplo: calcular la derivada de  .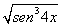
Puesto que sabemos calcular la derivada de una raíz, la derivada de una
potencia cúbica, la derivada de la función seno y la derivada de 4x,
estamos en condiciones de realizar cuidadosamente esta derivada: |
|
|
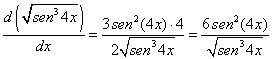