| Si bien el concepto de derivada nace de una idea
dinámica o de movimiento (a traves del tiempo), desde el punto de vista
rigurosamente analítico la derivada de una función nos entrega las
propiedades fundamentales de dicha función. |
| En lo que sigue en esta sección iremos viendo las
características de una cierta función y verificar si la derivada
puede describir tales características. |
| Consideremos una sencilla función polinómica |
|
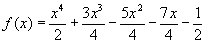 (1)
(1)
|
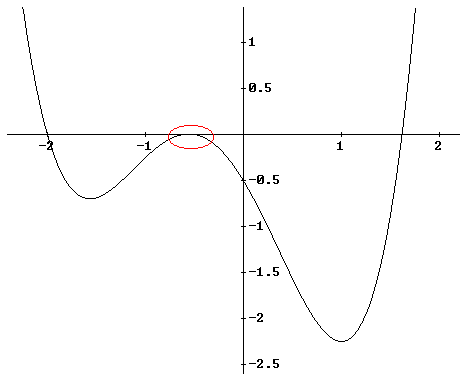
| La gráfica de esta función viene dada por |
|
|
| Esta función tiene cuatro raíces reales, y por
problemas de escala no se puede vislumbrar claramente las dos raíces
que se encuentran en el intervalo (-1, 0) marcado con una elipse roja..
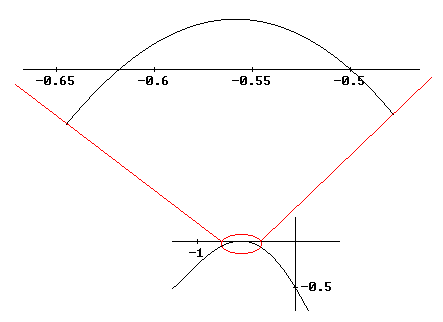
Si aplicamos un zoom en esa zona vemos lo siguiente |
|
|
| Se puede calcular (con el software DERIVE, por ejemplo)
que las raíces de esta función son: |
|
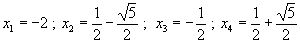
|
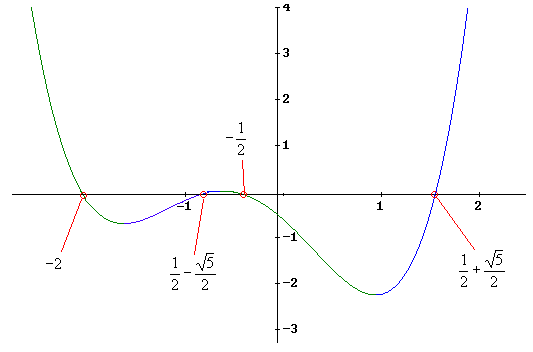
| Si ubicamos estos puntos en la gráfica, nos queda |
|
|
| donde hemos marcado de color verde la zona en que la
función es decreciente y de color azul la zona en que la
función es creciente. Haga click en esas zonas. |
| La derivada de la función (1) es |
|
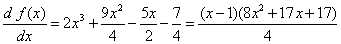 (2)
(2)
|
| No resulta complicado verificar, mediante el DERIVE por
ejemplo, que esta derivada (2) es positiva en los intervalos: |
|
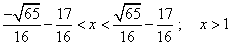
|
| y que justamente corresponden a los dominios de la
gráfica en los sectores de color azul. |
| Tampoco resulta complicado verificar que la derivada (2)
es negativa en los intervalos |
|
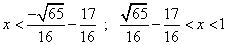
|
| y que corresponde al dominio de la gráfica que está de
color verde. |
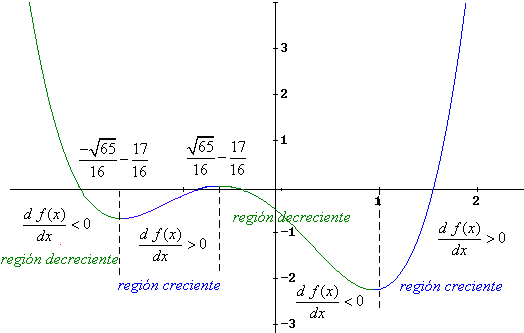
| El resumen de lo expuesto en este ejemplo se puede ver en
la siguiente gráfica |
|
|



