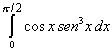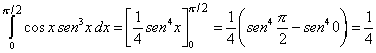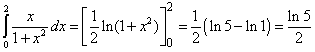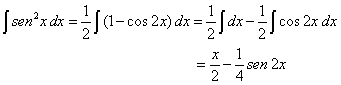| Para poder integrar a "lápiz y papel" se
requiere cierta experiencia con derivadas, algo de suerte y ciertas
técnicas clásicas para integrar. Lamentablemente, muy a menudo, se
confunde la técnica de integración con la matemática misma que trata
sobre el cálculo de integrales (es decir, se confunde algoritmo con
matemática). |
| Por alguna extraña razón estamos interesados en el
cálculo de la integral siguiente |
|
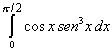
|
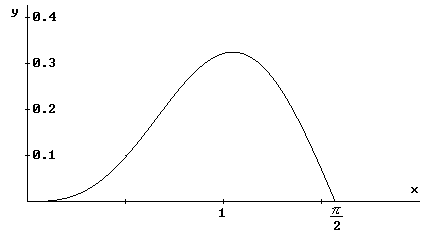
| La gráfica de la función f( x ) = cos
x sen3 x entre los valores 0 y p
es como sigue: |
|
|
| De tal forma que la integral pedida corresponde al área
bajo la curva entre los valores 0 y p.
Pareciera una integral bastante complicada, sin embargo debemos recordar
que |
|
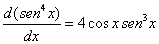
|
| de tal forma entonces que |
|
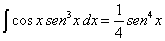
|
| y por lo tanto la integral definida solicitada es |
|
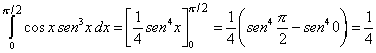
|
|
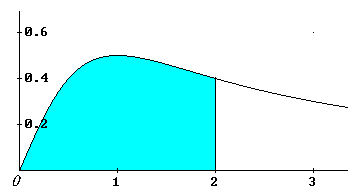
| Veamos otro ejemplo: Calcular el área acotada por las
curvas y = x / (1 + x2), y = 0, x
= 0 , x = 2. |
| Lo que se pide entonces es la integral siguiente |
|
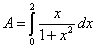
|
| que es el área que se indica en el siguiente gráfico |
|
|
| El cálculo de esta integral es relativamente sencillo si
recordamos que |
|
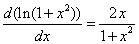
|
| de modo que |
|
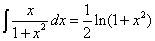
|
| y por lo tanto |
|
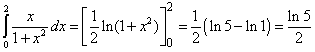
|
|
| En resumidas cuentas, lo que se quiere decir en esta
sección que hay una gran variedad de funciones en la que su integral es
casi inmediata en cuanto y en tanto seamos capaces de reconocer su
"anti-derivada", es decir seamos capaces de determinar que la
función que queremos integrar proviene de una derivada que conocemos.
Lamentablemente, no siempre es así. Otras veces tenemos que acudir a
subterfugios algebraicos que se fundamentan en un reemplazo algebraico
adecuado (con mucha suerte) para la resolución. Veamos el siguiente
ejemplo. |
| Ejemplo. Se quiere integrar la función |
|
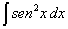
|
| Para esto acudimos a la identidad trigonométrica |
|
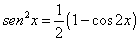
|
| y de este modo |
|
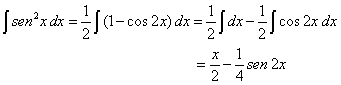
|