El concepto de integral

Con cierta frecuencia, los alumnos de cálculo confunden el concepto de integral con "antiderivada", que en su justo rigor no es incorrecto, pero lamentablemente se especializan tanto, y seguramente en esto el profesor de cálculo es cómplice, en calcular una ristra de "antiderivadas" de funciones que olvidan el concepto mismo de derivada, y en definitiva olvidan su adecuado uso. Con mucha dosis de suerte, reconocen también en la integral una suerte de "cálculo de área bajo la curva" (entendiendo que esta curva es la representación gráfica de una función no negativa), cuestión que tampoco es incorrecta. Ahora bien, en este curso intentaremos dar el amplio concepto de integral, de tal manera que abarque como corolario su utilización como "antiderivada", fundamentalmente para la resolución de ecuaciones diferenciales, y su utilización geométrica como el cálculo del área bajo la curva, y en esta aplicación lo ligaremos con conceptos de la teoría de la probabilidad.

Creo que podemos dedicar más tiempo en el concepto mismo de la integral, sacrificando una buena dosis de tiempo en la enseñanza de las instrucciones para las decenas y centenas de fórmulas de integración que existen, toda vez que hoy por hoy ya no es absolutamente necesario, ni menos manejar "tablas de integración", pese a que en algunos programas de cálculo estas "tablas de integración" permanecen inmutables en el tiempo. Más bien aprovecharemos la tecnología que democratiza el cálculo de integración, puesto que se puede obtener en milésimas de segundo cualquier integral de cualquier función por muy compleja que sea en las decenas de buenos softwares matemáticos que existen.

El flujo de agua. Supongamos que en un recipiente, como lo indica la figura 1, está cayendo agua a través de un grifo. Supongamos además que el flujo de agua, o caudal, que sale del grifo es de I m³ / seg. El agua que cae hacia el recipiente está formando un determinado volumen que varía con el tiempo. Pues bien, deseamos saber el volumen de agua que se ha formado desde el tiempo t = a seg hasta el tiempo t = b seg. De otra forma queremos saber el volumen de agua que se ha obtenido entre los tiempos a y b mientras el caudal de agua fluye constante en un valor I. La respuesta es naturalmente

Volumen = I ( b - a)

esto es el caudal por el tiempo transcurrido.

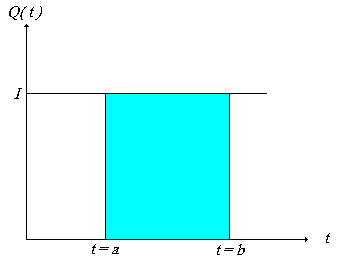
Desde el punto de vista geométrico el valor I ( b - a) viene a ser el cálculo del área de un rectángulo de altura I con base (b - a).

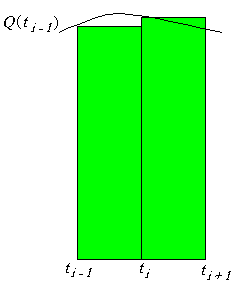
De otra forma consideremos la función constante Q( t ) = I, y realicemos su gráfica en el plano cartesiano como lo indica la figura 2.

Figura 1

Podemos observar que el área del rectángulo de color corresponde numéricamente a la cantidad de volumen obtenido por el caudal I en el intervalo de tiempo [a, b].

Vamos a suponer ahora que el caudal no es completamente constante, sino que tiene el siguiente comportamiento, durante el intervalo de tiempo [a, b] el caudal vale Q( t ) = I₁, y durante el intervalo de tiempo (b, c] el caudal es de Q( t ) = I₂. Donde I₁ e I₂ son flujos constantes, es decir a partir del tiempo t = b hubo un cambio instantáneo de caudal.

Nos interesa calcular el volumen conseguido en el intervalo de tiempo [a, c].

La situación gráfica se indica en la figura 3.

En este caso, el volumen obtenido es de

Volumen = I₁ ( b - a ) + I₂ ( c - b )

y geométricamente coincide con la suma de las áreas de los dos rectángulos.

Supongamos ahora que la función Q( t ) no es constante en el intervalo [a, b], como lo indica la Figura 4.

Figura 4

Figura 2

Figura 3

¿Cómo podríamos calcular el volumen de agua?

Vamos a formar pequeños rectángulos de la siguiente manera, la base b - a la vamos a subdividir en intervalos de la misma longitud, de tal manera de formar n subintervalos de longitud (b - a) / n, estos subintervalos entonces formarán la siguiente partición

a = x₀ < t₁ < ... < t _i_{- 1} < t_i < t _{i + 1} < ... < t _n_{-
1} < t_n = b

de tal forma que

Dt_i = t_i - t _{i - 1} = (b - a) / n

y la altura del i-ésimo rectángulo será igual a Q( t _i_{- 1} ), de tal forma que el área de cada subrectángulo es Q( t _i _-1 )Dt_i.

La construcción de los n subrectángulos lo presentamos en la Figura 5, y en la Figura 6 se observa el i-ésimo subrectángulo amplificado de base t_i - t _{i
- 1} y de altura Q( t _{i - 1} ).

Figura 5

Figura 6

De tal forma que el volumen de agua aproximada que se formará durante el intervalo de tiempo [a, b] es la suma de las áreas de todos estos subrectángulos, esto es

la elección de los n subrectángulos fue en cierto modo arbitraria, mientas más fina sea la partición, esto es mientras más subrectángulos formemos mejor será la aproximación del cálculo del área bajo la curva. Entonces se define la integral de la función Q( t ) entre a y b como

y que para este ejemplo particular corresponde al volumen de agua formado por el caudal Q( t ) en el intervalo de tiempo [a, b] , y que geométricamente corresponde al área bajo la curva de Q( t ) en el intervalo [a, b].