| Generalizando lo que vimos en la anterior sección, tenemos que si f( x ) es una función no negativa, definida en un intervalo [a, b], entonces definiendo una partición en el intervalo [a, b] de la forma |
|
x0 = a < x1 < x2 < ... < xn = b |
|
|
| de tal modo que cuando |
|
|
| y si elegimos arbitrariamente |
|
|
| y formamos la suma |
|
|
| se tiene que el área bajo la curva de f( x ) entre los valores a y b está dada por |
|
|
| Observe que el valor de la derecha de esta última ecuación representa un número, y que se denota por "la integral de f( x ) entre los valores a y b". |
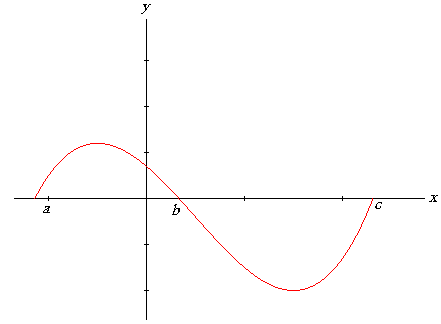
| Sin embargo, en la construcción de esta integral se puede relajar la exigencia de que la función f( x ) debe ser no negativa y realizar los cálculos sobre la partición en el intervalo de definición de la función. Por ejemplo f( x ) puede ser una función con la siguiente gráfica |
|
|
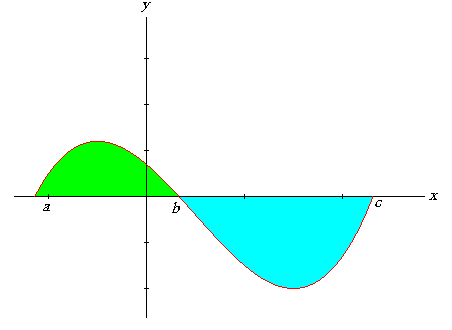
| donde se entiende que la integral en el dominio [b, c] tendrá un valor negativo, pero su valor absoluto (sin el signo menos) es geométricamente el área de la región determinada por la gráfica de f( x ) y el segmento [b, c]. De otra forma, la integral de la función f( x ) en el intervalo [a, c] corresponde numéricamente, en este ejemplo, a la diferencia entre la región verde menos la región celeste que se muestra en la siguiente gráfica |
|
|
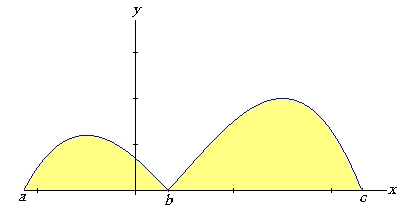
| Que es un resultado absolutamente diferente si integramos la función valor absoluto de f( x ), cuya gráfica viene a ser de la forma |
|
|
| y el valor de las dos áreas amarillas corresponde a la integral |
|
|
| Las propiedades más importantes sobre integrales |
| No resulta para nada complicado demostrar las siguientes propiedades de las integrales. |
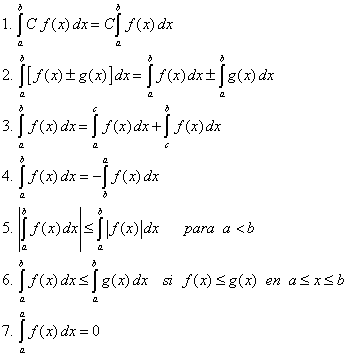 |