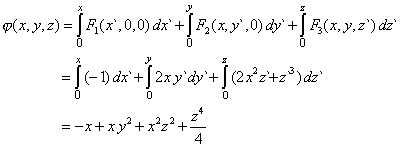|
En sección anterior identidades en el cálculo vectorial establecimos que |
|
div rot F = Ñ . Ñ x F = 0 (1) |
|
rot grad j = Ñ x Ñj = 0 (2) |
| Observemos los campos generados por F y j que actúan en ambas identidades, esto es G = Ñ x F y H = Ñj. Para cada caso se dice que F es el potencial vectorial de G y j es el potencial escalar de H. |
| ¿Cuándo un determinado campo posee potencial vectorial o escalar? |
| Teorema 1. Si F es un campo vectorial tal que div F = 0 entonces existe un campo vectorial A tal que Ñ x A = F, o de otra forma rot A = F. (Nota: el campo vectorial A se dice potencial vectorial de F, y no es único) |
| Demostración. Construiremos un campo vectorial A tal que Ñ x A = F, y de tal forma que, por (1), se satisfaga que |
|
|
| Las componentes de A deben cumplir entonces |
|
|
| Puesto que la solución no es única, hagamos arbitrariamente A3 = 0, de modo que nos quedan las ecuaciones |
|
|
| Integrando las dos primeras ecuaciones, obtenemos |
|
|
| donde M y N son funciones escalares arbitrarias ("constantes" de integración). Con estas funciones armamos la tercera ecuación que no se ha involucrado aún, esto es |
|
|
| De la igualdad en (3) reemplazamos el integrando, |
|
|
| Como N y M son arbitrarias hacemos M = 0, entonces obtenemos una expresión para N, esta es |
|
|
| Hemos obtenido expresiones para las componentes del campo vectorial A, de (4) tenemos que |
|
|
| Nota: los valores x0 y z0 son arbitrarios. |
| Ejemplo. Pruebe si el campo F = (x - y) i + (y + xz) j + (y - 2z) k tiene un potencial vectorial y encuentre uno. |
| No hay problema en probar que div F = 0. Ahora aplicando directamente las fórmulas dadas en (5) se tiene que |
|
|
| Luego una solución como potencial vectorial es |
|
|
| Teorema 2. Si F es un campo vectorial tal que rot F = 0 entonces existe un campo escalar j tal que F = Ñj |
| Demostración. Por hipótesis se cumple que |
|
|
| Vamos a construir la función escalar j. En efecto, se debe cumplir que |
|
|
| Integrando la última ecuación, |
|
|
| donde P( x, y) es una función arbitraria y (x0, y0, z0) un punto fijo. De la ecuación (8) obtenemos sendas derivadas parciales respecto de x e y, |
|
|
| Remplazamos los integrandos de estas dos ecuaciones en virtud de (6), y obtenemos |
|
|
| Esta sustitución nos permite una integración directa, |
|
|
| Ahora utilizando las ecuaciones en (7), tenemos que |
|
|
| Integrando la segunda ecuación, |
|
|
| Ahora derivamos esta función respecto de x, y utilizando la primera ecuación en (9) |
|
|
| y reemplazando el integrando por la última ecuación de (6), nos queda |
|
|
| de modo que |
|
|
| Recapitulando, de (8), (10) y (11) se concluye que |
|
|
| En definitiva, un potencial escalar está dado por |
|
|
| Ejemplo. Encontrar un potencial j para F = (y2 + 2xz2 - 1) i + 2xy j + (2x2z + z3) k |
| Un cálculo rápido nos permite verificar que el rotor de este campo es el vector nulo. Utilizando la fórmula obtenida en (12) y eligiendo el punto (x0, y0, z0) = (0, 0, 0), |
|
|
| Se verifica que el gradiente de este campo escalar es precisamente F. |
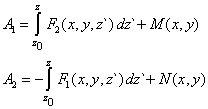 (4)
(4)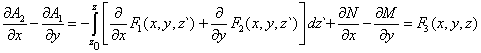
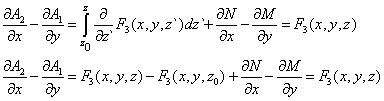
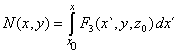
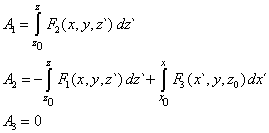 (5)
(5)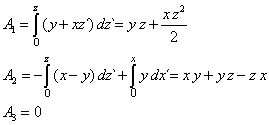
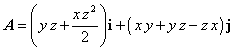
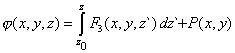 (8)
(8)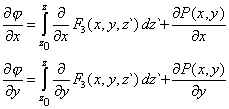
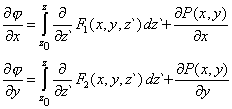
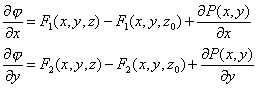
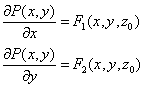 (9)
(9)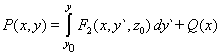 (10)
(10)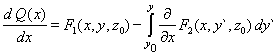
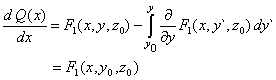
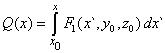 (11)
(11)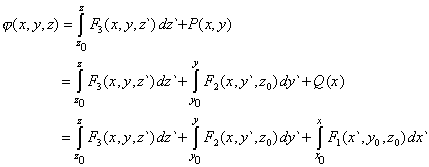
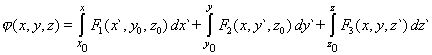 (12)
(12)