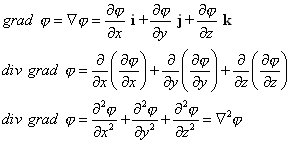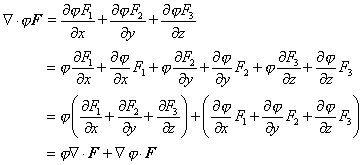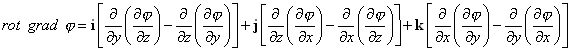| En base a las tres operatorias que hemos definido hasta el momento, a saber el gradiente de un campo escalar, la divergencia de un campo vectorial y el rotor de un campo vectorial, se pueden construir una serie de identidades cuya manipulación facilitará posteriores desarrollos del cálculo vectorial, así como las aplicaciones físicas. Tengamos en mente que si j es un campo escalar, y F un campo vectorial, y tenemos el operador Ñ |
|
|
| entonces grad j = Ñj , div F = Ñ . F , rot F = Ñ x F. Además recordemos que Ñ2 tiene sentido si lo interpretamos como el producto punto del (seudo) vector Ñ consigo mismo, esto es |
|
|
| De la operatoria (1) surge una ecuación notable con variadas aplicaciones en la teoría de la electricidad, magnetismo, óptica, gravitación, difusión, fluidos dinámicos, acústica y elasticidad, que es la llamada ecuación de Laplace, y consiste en encontrar un campo escalar j tal que se satisfaga |
|
Ñ2j = 0 (2) |
| Antes de ver una solución para la ecuación de Laplace, presentamos la primera identidad vectorial de esta sección: |
|
Ñ2j = div grad j (3) |
| La demostración de (3) es como sigue: |
|
|
| Si j y F son campos escalares y vectoriales respectivamente, entonces jF es un campo vectorial, y por lo tanto es aplicable la divergencia y el rotor. Se tiene las siguientes identidades |
|
Ñ . jF = jÑ . F + Ñj . F (4) |
|
Ñ x jF = jÑ x F + Ñj x F (5) |
| Las demostraciones de ambas identidades se desarrollan de las propias definiciones de los operadores involucrados. Veamos el primer caso, |
|
|
| La identidad en (5) se demuestra de manera análoga, toda vez que la derivada de un producto cruz obedece la regla multiplicativa ordinaria de derivadas. |
| Otras dos importantes identidades para un campo escalar j y un campo vectorial F, siempre que tengan todas sus derivadas parciales al menos de segundo orden y sean continuas, son las que se anuncian a continuación: |
|
div rot F = Ñ . Ñ x F = 0 (6) |
|
rot grad j = Ñ x Ñj = 0 (7) |
| Demostraremos (6). Aplicando la definición directamente, obtenemos |
|
|
| y puesto que, por hipótesis, las derivadas de segundo orden cruzadas son iguales, se tiene que el segundo miembro de esta igualdad se anula, y con esto queda demostrado (6). La identidad en (7) se demuestra de manera análoga, aplicando la definición directamente tenemos |
|
|
| y nuevamente como las segundas derivadas cruzadas de j son iguales, se tiene que la resultante es el vector nulo. |
| Si G es un campo vectorial, entonces Ñ . G es la divergencia de G, sin embargo la expresión G . Ñ no es la misma, en rigor es un nuevo operador definido como |
|
|
| A continuación presentamos cuatro identidades que pueden ser útiles, |
|
Ñ x ( Ñ x F ) = Ñ( Ñ . F ) - Ñ2 F (8) |
|
Ñ . ( F x G ) = G . ( Ñ x F ) - F . ( Ñ x G ) (9) |
|
Ñ x ( F x G ) = ( Ñ . G )F - ( Ñ . F )G + (G . Ñ)F - ( F . Ñ)G (10) |
|
Ñ( F . G ) = F x ( Ñ x G ) + G x ( Ñ x F) + ( F . Ñ)G + ( G . Ñ )F (11) |
| Ejemplo. Sea W un vector constante y r = x i + y j + z k, calcular rot W x r. (Notemos que el campo vectorial W x r puede modelar la velocidad de un cuerpo en rotación rígida con velocidad angular W). Veamos la demostración, usando la identidad (10) |
|
Ñ x ( W x r ) = ( Ñ . r )W - ( Ñ . W )r + (r . Ñ)W - ( W . Ñ)r |
| puesto que las derivadas de una constante son ceros, se tiene que Ñ . W = 0 y (r . Ñ)W = 0, nos queda entonces |
|
Ñ x ( W x r ) = ( Ñ . r )W - ( W . Ñ)r = 3W - ( W . Ñ)r |
| pero como |
|
( W . Ñ)r = W1 i + W2 j + W3 k = W |
| se tiene que |
|
Ñ x ( W x r ) = 2W |