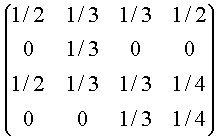, y es claro queTema: Probabilidades de transición de n-pasos
Una cadena de Markov está completamente definida por sus
probabilidades de transición de un paso, y la especificación de la distribución del
estado inicial del proceso. Sin embargo en el cálculo del proceso en el tiempo n, esto es
en el cálculo de P(n), fue estratégico el cálculo de la potencia n de la matriz de
Markov (resultado válido aún para matrices cuadradas infinitas); ahora bien, supongamos
que la matriz de Markov es M, y hemos obtenido la matriz potencia , y es claro que
Pero ahora, ¿Cuál es el significado para las cadenas de Markov que tiene la matriz potencia, y en particular la igualdad anterior? La respuesta amerita una definición. Definamos
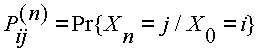
Que denota la probabilidad de llegar al estado j desde el estado i en n-pasos. Recordemos que estamos trabajando con cadenas de Markov estacionarias, lo que significa que la definición anterior es equivalente a
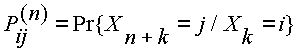
El principal resultado de esta probabilidad de n-pasos con las entradas de la matriz potencia, es el siguiente:
TEOREMA: Si M es la matriz de Markov asociada a una cadena de
Markov, entonces 
corresponde
a la entrada 
de la matriz 
El cálculo de la matriz potencia a menudo no es sencillo. Se entiende
como "sencillo" el hecho de no tener que hacer n iteraciones de multiplicación,
lo que significa encontrar una forma analítica para 
.
Al respecto, es clásico el resultado de que si M es una matriz diagonalizable, entonces existe una matriz P, tal que
Donde D es una matriz diagonal formada por los autovalores de la matriz M. Si es factible la última ecuación tendríamos que, en este caso
Ejercicio: Determine si la siguiente matriz es diagonalizable
