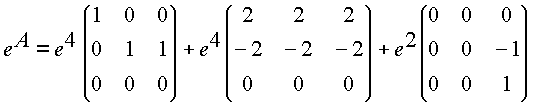Tema: Resolución Espectral de la potencia de una matriz (de Markov)
Objetivo: Entregaremos los resultados para obtener una expresión analítica para potencias de una matriz, aunque ésta no sea diagonalizable.
Sea M una matriz cuadrada de orden n no necesariamente de Markov, de manera que su polinomio minimal sea
Supongamos que tenemos una función f definida sobre el conjunto de los números complejos, se dice que esta función está definida sobre el espectro de la matriz M si existen los valores de
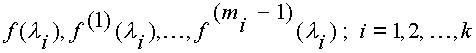
Donde el supraíndice j denota la j-ésima derivada. Con lo anterior establecemos el siguiente teorema sin demostración:
TEOREMA. Si 
está
definida en el espectro de M entonces
existen matrices 
independientes
de 
tales que
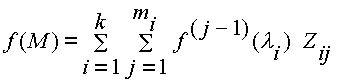
Las matrices se llaman las matrices componentes de la matriz M, y puede ser de interés decir que ellas son
linealmente independientes (esto es, ninguna es combinación lineal del resto) y además
conmutan en el producto con la matriz M.
Veamos un ejemplo, consideremos una matriz no markoviana
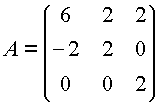
no es difícil concluir que el polinomio minimal es
Luego para cualquier función definida en el espectro de A se tiene, en virtud del teorema
anterior, que
y puesto que las matrices son independientes de la función , elegimos de forma conveniente funciones definidas
en el espectro de A. Consideremos
Manipulando algebraicamente se concluye que
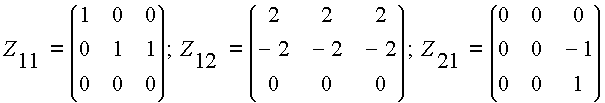
Todos los cálculos anteriores se pueden efectuar con el software DERIVE, para eso oprima aquí.
Ahora bien para cualquier función f definida en el espectro de A se tiene
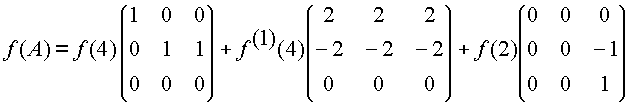
en particular para 
se tiene que
