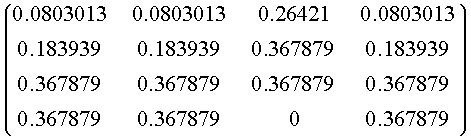
Tema: Simulación de cadenas de Markov
Objetivo: Enseñar técnicas de simulación, mediante el lenguaje de Forrester, para el modelamiento de procesos markovianos. Comparar los resultados obtenidos en la modelación con los resultados ergódicos de los procesos makovianos.
En la clase pasada, observamos que la matriz de Markov que regula el proceso del ejemplo de Stock está dada por
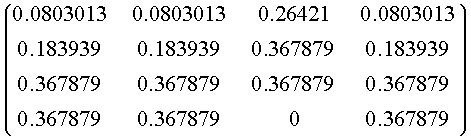
Si se tiene que el vector de distribución inicial es:
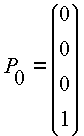
Entonces la distribución en el tiempo n-ésimo estará dada por:
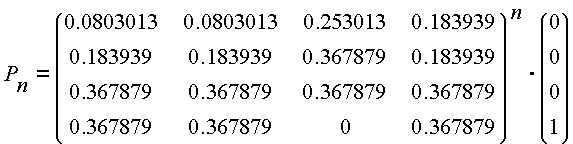
En particular se tiene que
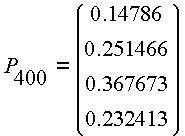
Lo que indicaría que habría una estabilización asintótica de esta probabilidad (esto lo veremos con más fundamentos en la teoría ergódica de matrices de Markov).
Lo que realizaremos ahora es una simulación del stock, mediante la técnica de Forrester utilizada en cursos de Dinámica de Sistemas (para recordar esta técnica, o aprender de ella, puede consultar la página Dinámica de Sistemas con aplicaciones a la Estadística y la Ecología.
La técnica a usar es bastante sencilla, consideraremos como variable de estado (en el sentido de Forrester) los posibles valores (de estado) que puede tomar la cadena de Markov, esto es {0,1,2,3}, y que se verá alterado por un flujo de salida o demanda, regulada por una distribución de Poisson; y por un flujo de entrada, que representará el abastecimiento del Stock según la política (s,S). Es decir, simularemos una situación real de Stock cuya dinámica la entregan las reposiciones y las ventas. En esta dinámica de observar lo que tenemos en Stock en un período determinado, contaremos la frecuencia de los valores de la variable de estado, y así su frecuencia relativa, que para un gran número de simulaciones estas frecuencias relativas deberán estar muy próximas del valor dado por
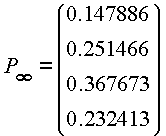
La modelación se ha efectuado bajo el ambiente STELLA, y se puede bajar desde el Modelo del Stock (comprimido en zip, realizado en Stella 5.0)