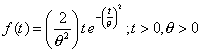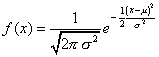Esta distribución tiene varias aplicaciones en muchos problemas de confiabilidad de tipo combinatorio. Esta distribución es bastante útil cuando se relaciona con la probabilidad de salida tal como el número total de fallas en una secuencia de k ensayos, donde cada ensayo tiene dos posibles resultados (falla o no falla) y la probabilidad de falla es la misma para cada ensayo. la función de densidad discreta o función de cuantía está definida por

p es la probabilidad de falla para cada ensayo; i es el número de fallas en los k ensayos. La función de distribución acumulativa está dado por

2.2 La distribución de Poisson

Esta es otra distribución utilizada en confiabilidad cuando uno está interesado en la ocurrencia de un número de eventos que son del mismo tipo. la ocurrencia de cada evento es denotado por un punto en la escala de tiempo, donde cada evento representa una falla. la función de distribución está definida por

donde l es la constante de falla (o razón de falla), t es el tiempo. la función de distribución acumulativa es

2.3 La distribución exponencial

Esta es la distribución más ampliamente utilizada en confiabilidad en ingeniería, debido a que muchos procesos en ingeniería muestran una razón constante de riesgo durante su vida útil. Además es analíticamente manejable en el análisis de confiabilidad. la función de densidad continua está definida por

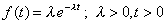
l es la razón constante de falla por unidad de tiempo. Su función de distribución acumulativa es

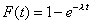
No resulta complicado demostrar que si T es una variable aleatoria que sigue esta densidad entonces su esperanza es

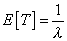
2.4 la distribución de Rayleigh

Esta distribución es usada en trabajos de confiabilidad asociados a problemas en teoría del sonido. Su función de densidad está dada por

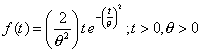
La función de distribución acumulada está dada por

Si T es una variable aleatoria que sigue esta ley de probabilidad se puede demostrar que su esperanza es

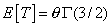
Siendo G ( ) la función gamma definida por

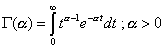
2.5 La distribución de Weibull

Esta distribución puede ser usada para representar varios fenómenos físicos. Su función de densidad está dada por

donde b y q son los parámetros de forma y escala, respectivamente. La función de distribución acumulativa es como sigue

Si T es una variable aleatoria que sigue esta función de probabilidad, entonces su esperanza es

Observemos que cuando b = 2, caemos en la distribución de Rayleigh.

2.6 La distribución general

Esta distribución puede ser usada para representa la función de riesgo "bañera". daremos esta vez primero la función de distribución:

donde k tiene valores entre 0 y 1 y el resto de los parámetros son todos positivos, y por supuesto t > 0. la función de densidad se puede obtener por derivación.

Teoría de la confiabilidad

Distribuciones de probabilidad

2.1 La distribución binomial

2.2 La distribución de Poisson

2.3 La distribución exponencial

2.4 la distribución de Rayleigh

2.5 La distribución de Weibull

2.6 La distribución general

2.7 La distribución normal