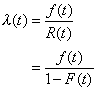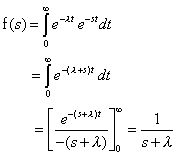|
|
|
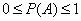
|
|
|
|
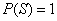
|
|
|
|
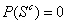
|
|
|
|
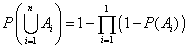
|
| donde Ai es el
i-ésimo evento y P(Ai) es la probabilidad de ocurrencia del
i-ésimo evento. |
| Para n =2 la ecuación
anterior se reduce a |
|
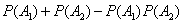
|
- La probabilidad de la unión de n eventos
mutuamente excluyentes es
|
|
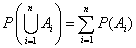
|
1.2 Definiciones útiles
|
La función de distribución
|
| La función de
distribución acumulativa de una variable X está definida por |
|
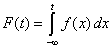
|
| donde t
es el tiempo, f(x) es la función de
densidad. |
La función de confiabilidad
|
| Está expresada por |
|
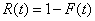
|
|
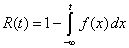
|
| siendo R(t) la función de
confiabilidad. Y observe que su interpretación es bastante sencilla:
viene a ser la probabilidad de que la variable aleatoria (el tiempo
aleatorio) dure más allá de un tiempo t. ¿Se da cuenta? |
La función razón de riesgo
|
| Está definida por |
|
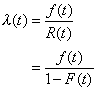
|
| siendo l(t)
la función razón de riesgo. |
Transformada de Laplace
|
| La transformada de Laplace
de la función f(t) está definida por |
|
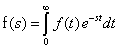
|
| donde s es la variable de
la transformada de Laplace, t es la variable tiempo, y f(s)
de la transformada de Laplace de f(t) |
Ejemplo
|
| Si f(t) = e - lt
la transformada de Laplace de esta función se calcula del siguiente
modo: |
|
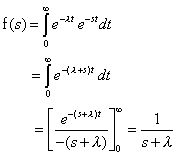
|
| Nota: siempre que l
+ s > 0. |
| Para una tabla de
transformada de Laplace acuda al libro base, página 7 capítulo
2. |
El teorema del valor final
|
| Si el siguiente límite
existe entonces el teorema del valor final establece que |
|
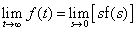
|
El valor esperado
|
| El valor esperado de una
variable aleatoria continua T, E [ T
], está dado por |
|
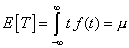
|