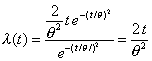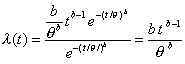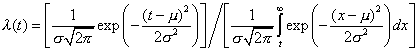| La función razón de riesgo es
fundamental en teoría de la confiabilidad, y conforme a la definición
que dimos en la primera sección está razón depende del modelo de
densidad que estemos utilizando. Habíamos definido la función razón
de riesgo como el cuociente |
|
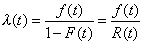
|
| siendo f( t )
y F( t ) la función de densidad y de
distribución respectivamente. Sin embargo rigurosamente hablando, tiene
un sentido más intuitivo su definición conceptual como sigue, |
|
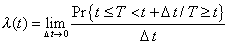
|
|
Siendo T la
variable aleatoria que indica el tiempo de funcionamiento del ítem bajo
estudio. No resulta complicado demostrar que esta definición es
equivalente a la anterior. De tal manera que el valor l(t)Dt
es aproximadamente la probabilidad de que el ítem siga funcionando
durante el intervalo de tiempo (t , t
+ Dt) dado
que ha funcionado sin falla hasta el tiempo t. |