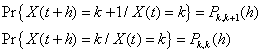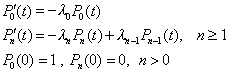| Vamos a estudiar sistemas que
eventualmente pueden pasar por etapas de "degradación" antes
de colapsar definitivamente mediante cadenas de markov, recordemos que
esta situación se vio incipientemente en la sección
12. Pero esta vez por razones analíticas consideraremos los estados
infinitos para así poder establecer las ecuaciones diferenciales que
regulan el sistema, para posteriormente truncar el proceso en un estado
finito absorvente, que significará el estado de falla del sistema.
Conceptualmente será un proceso de Markov el cual solo podrá avanzar,
o quedarse en el estado en que está, en tiempos infinitesimales. El
mejor modelo que se adecua a este objetivo es el llamado proceso de
nacimiento puro. |
| Proceso de nacimiento Puro |
|
Consideremos una sucesión de números positivos {lk}.
Se define un proceso de nacimiento puro como un proceso de Markov que
satisface los siguientes postulados: |
|

|
|
X( t ) denota el valor de estado que
puede tomar el proceso en el tiempo t. En lo que respecta a la
teoría de confiabilidad el valor de estado denotará el estado de
degradación en que incurre el sistema, entendiendo el 0 como el estado
óptimo, y los sucesivos estados como etapas de degradación creciente,
hasta llegar a un estado N que significará el estado de colapso, no
obstante con el objeto de aplicar directamente la teoría de los
procesos de nacimiento puro, consideraremos el espacio de estado
infinito {0, 1, 2, ...}. |
| El término o1,k(h) y o2,k(h)
son "infinitesimales" de orden h, esto es |
|
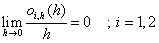
|
| Un ejemplo de función infinitesimal
es o(h) = h2. La función o(h) = h no es infinitesimal de
orden h. |
| Además podemos definir |
|
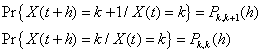
|
| diciendo con esto que el proceso de
Markov es estacionario., y estos valores corresponden a los valores del
lado izquierdo de (i) y (ii), diciendo con esto además que las
funciones infinitesimales no dependen de t. |
| Definamos |
|

|
| Teorema. El proceso de
nacimiento puro satisface el siguiente sistema de ecuaciones
diferenciales: |
|
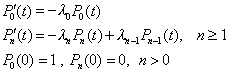
|
| La demostración se deja como
ejercicio: Se utiliza la ley de la probabilidad completa, la propiedad
de Markov y el postulado (iii). |
| La primera ecuación diferencial se
puede resolver directamente, y esta es |
|
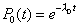
|
|
Las restantes se calculan recurrentemente, y la
expresión general está dada por |
|
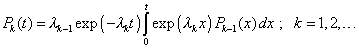
|
|
Tarea: haga las modificaciones pertinentes para
detener el proceso en un estado absorvente N. |
| Para asegura la validez del proceso en
la resolución de las ecuaciones diferenciales que determinan Pn(t),
esto es de que efectivamente |
|
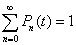
|
| los valores lk
deben satisfacer la condición |
|
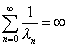
|
|
|