| Para un proceso de nacimiento puro,
definamos Tk como el tiempo entre el k - ésimo y (k + 1 ) -
ésimo nacimiento; de modo que |
|
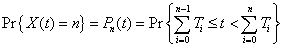
|
| De otra forma, los Tk son
tiempos de estera entre nacimientos (interprételo como la llegada de
una componente a reparación o complementariamente a la falla de una
componente) |
| De tal modo que |
|
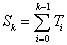
|
| es el tiempo en el cual el k - ésimo
nacimiento ocurre. |
| En la sección anterior habíamos
visto que P0(t) = exp( - l0t
), de modo que |
|
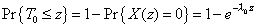
|
| es decir T0 tiene una
distribución exponencial de parámetro lo. De los postulados del
proceso de nacimiento puro que los Tk , k > 0, también
tienen una distribución exponencial con parámetro lk,
y estos tiempos son mutuamente independientes. Los cálculos precisos
escapan de los objetivos de este curso, pero se puede demostrar que la
función característica de Sn está dada por |
|
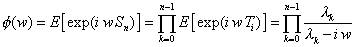
|
| De modo que cuando lk
= l, se reconoce
que Sn tiene una distribución gamma de parámetro n, y con
esperanza n / l. |
|