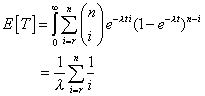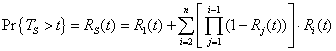| Redes (r, n) |
| Se trata de un sistema con n
componentes independientes, de tal forma que el sistema funciona toda
vez que funcionen al menos r componentes. Es lo que se podría decir un
sistema redundante.
Si suponemos que la función de confiabilidad de cada componente es la misma, digamos R, y además las componentes son independientes, entonces la confiabilidad del sistema completo, R(r,n), se obtiene fácilmente, y viene dada por |
|
|
| Para un sistema de este tipo donde cada componente tengo una razón de riesgo constante l, esto es cuando R = exp { - l t }, entonces |
|
|
| y entonces el tiempo medio de falla para el sistema completo es |
|
|
| La complejidad del problema viene cuando las componentes del sistema, manteniendo su independencia, no tienen la misma función de densidad de probabilidad de falla, y por ende cada componente tiene distinta función de confiabilidad. No obstante, la función de confiabilidad en tal situación se puede deducir del siguiente trabajo sobre "confiabilidad en los marcadores genéticos": aquí. |
| Los cálculos de razón de riesgo y tiempo esperado de falla son relativamente sencillos para el caso en que las componentes sea independientes e idénticamente distribuidas, sin embargo no son tan sencillos los cálculos para el caso en que las componentes sean independientes pero sus funciones de confiabilidad no necesariamente sean iguales. |
| Suponga que ei(t) es la función de confiabilidad para la componente i-ésima, calcule entonces la función de confiabilidad R(t) para un sistema (r, n), y además el tiempo medio de falla y la función de riesgo. |
| Redundancia en espera |
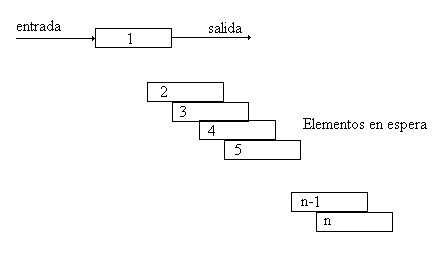
| Supongamos un sistema que opera con una componente, sin embargo hay m componentes que están en espera listo para reemplazar a la componente que está operando en caso de falla. De otra forma el sistema tiene (m + 1) componentes, y toda vez que una componente falla un switch automático opera una de las componentes en espera (stand by) para que el sistema siga funcionando. Evidentemente el sistema dejará de funciones si fallan todas las componentes. Para intentar resolver el problema inicialmente, supongamos que las componentes son independientes y cada componente tiene función de confiabilidad Ri(t). Y el objetivo es encontrar la confiabilidad del sistema. Observemos el siguiente esquema: |
|
|
| Si TS es el tiempo de falla del sistema, y las funciones de confiabilidad de cada componente están dadas por Ri(t), entonces la función RS(t) de confiabilidad está dada por |
|
|
| Utilice este resultado para los casos en que las componentes se distribuyen idénticamente según las distribuciones clásicas que hemos estudiado hasta ahora. |