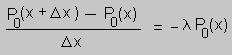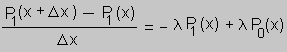La distribución de Poisson

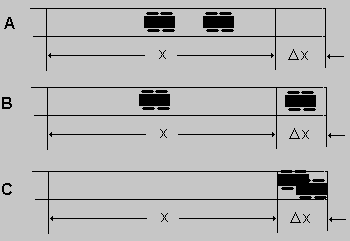
1) En un segmento de carretera de longitud Dx la probabilidad de encontrar uno y solo un vehículo es proporcional a la longitud Dx, esto es l Dx; y la probabilidad de encontrar más de un vehículo en el segmento de carretera de longitud Dx es cero.

2) Los eventos de encontrar o no encontrar vehículos en segmentos de carretera no traslapadas son independientes.

Muy bien, con estos dos postulados vamos a construir el modelo probabilístico de Poisson. Tal vez sea necesario un comentario. El postulado uno se conoce como la "ley de los raros eventos"; y hay una variedad de ejemplos de la vida diaria que naturalmente lo cumplen. Imaginemos la gente que va a ponerse en la cola de una caja de un banco. Parece claro que las personas que llegarán a la fila en un instante de tiempo pequeñísimo como Dt (por ejemplo milésima de segundo) no serán más de una, es decir que los únicos eventos probables son 0 personas, o 1 persona. De igual manera, si consideramos un metro cuadrado de región de mar, los únicos eventos probables de encontrar tiburones en esa área es ningún tiburón, o 1 tiburón. 

El segundo postulado se conoce como la propiedad de los incrementos independientes.

Queremos contestar la pregunta, ¿cuál es la probabilidad de encontrar n vehículos en la carretera de longitud x?

Para contestar esta pregunta, definamos la expresión P_n(x), que denotará la probabilidad de encontrar n vehículos en un segmento de carretera de longitud x.

Para fijar ideas vamos a calcular P₀(x). Y para esto vamos a considerar una carretera de longitud x + Dx como se indica en la figura 2. Las únicas opciones para que no se tenga ningún vehículo en una carretera de longitud x+Dx es que no haya ningún vehículo en el segmento x , como tampoco ningún vehículo en el segmento Dx . Y puesto que lo que ocurra en ambos segmentos, por el postulado 2, son independientes, se tiene que

P₀(x+Dx) = P₀(x) P₀(Dx)

P₀(x+Dx) = P₀(x) (1 - l Dx)

P₀(x+Dx) = P₀(x) - l P₀(x)Dx

hacemos Dx g 0, y nos queda la ecuación diferencial

P₀^'(x) =  - l P₀(x)

con condición inicial P₀(0) = 1. La solución claramente es

P₀(x) = e ^{- lx}

Vamos a calcular ahora P₁(x). Igual que antes vamos a considerar una carretera de longitud    x + Dx. Las opciones exhaustivas que pueden ocurrir para encontrar un vehículo en esa carretera de longitud x + Dx se entregan en la figura 3. De manera tal que, en virtud de la independencia de segmentos de carretera no traslapados se tiene que

P₁(x + Dx ) = P₁(x) P₀(Dx) + P₀(x) P₁(Dx)

Es decir

P₁(x + Dx ) = P₁(x) (1 - l Dx) + P₀(x) l Dx 

hacemos Dx g 0, y nos queda la ecuación diferencial

P₁^'(x) + l P₁(x)=  l P₀(x)

con condición inicial P₁(0) = 0. La solución es

P₁(x) = e ^{- lx} (lx)

Figura 1

Figura 2

Figura 3

Figura 3

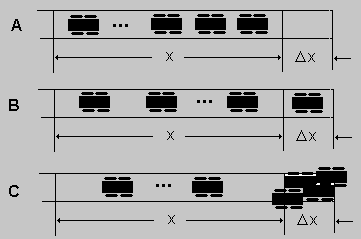
Figura 4

Vamos al cálculo de P₂(x). De manera análoga, estudiamos la situación en una carretera de longitud x + Dx, y vemos que las únicas opciones para encontrar dos vehículos se indican en la figura 3. Sin embargo el suceso C tiene probabilidad 0 de ocurrir, en virtud del primer postulado, de manera que

P₂(x + Dx ) = P₂(x) P₀(Dx) + P₁(x) P₁(Dx)

y actuando de manera similar llegamos a la ecuación diferencial

P₂^'(x) + l P₂(x)=  l²x e ^{- lx}

con condición inicial P₂(0) = 0. La solución es

P₁(x) = e ^{- lx} (lx)²/ 2!

Ahora estamos en condiciones de resolverlo en forma general. Vamos a considerar que tenemos n vehículos en la carretera de longitud x + Dx. La situación se describe en la figura 4.

En este caso, la figura 4 A, describe la situación de encontrar n vehículos en el segmento de carretera x, y o en el segmento Dx. La figura 4 B, de encontrar   n - 1 vehículos en x y 1 en Dx: Y finalmente las otras situaciones, descritas por C, en que con probabilidad nula se pueden encontrar más de un vehículo en Dx. En este caso la ecuación queda como

P_n^'(x) + l P_n(x)=  l P_n-1(x)

y cuya solución es

P_n(x) = e^-lx (lx)ⁿ / n!

El caso particular cuando  x = 1, es el que comúnmente se utiliza para describir la distribución de Poisson.