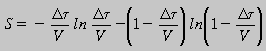Entropía y aleatorización

En general, para cualquier espacio de probabilidad, si un suceso tiene baja probabilidad, decimos entonces que raramente ocurre o es poco frecuente su ocurrencia. Podemos decir, entonces, que dicho suceso pertenece a la categoría de los sucesos "inesperados". Por el contrario, si tenemos un suceso con alta probabilidad, entonces es un suceso que ocurrirá con mucha frecuencia, de manera tal que no nos extrañara que dicho suceso ocurra. Diremos, en consecuencia, que no es un suceso inesperado.

Resumamos lo anterior en la siguiente definición natural: Si W es la probabilidad de ocurrencia de un suceso determinado, entonces lo "inesperable" del suceso se define como

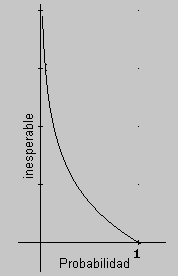
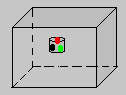
es decir el logaritmo natural de la probabilidad con signo menos, de tal forma que la medida de lo "inesperable" resulte positiva. En rigor, para cualquier suceso mientras menos sea su probabilidad, su "inesperabilidad" aumentará. Observe la figura 1.

A manera de ejemplo consideremos un recipiente cerrado de volumen V, de tal forma que contiene tres moléculas de un gas. Supongamos que tenemos fijada una subregión espacial de volumen igual al 10% del volumen V. Y estamos interesados en calcular la medida de lo inesperado de encontrar las tres moléculas en la subregión espacial. Observe la figura 2.

Si nuestro interés es medir lo "inesperado" de que las tres moléculas estén contenidos en la subregión espacial, tenemos que, para este caso,

y entonces

Por otro lado la medición de lo inesperado del suceso de que las tres moléculas se encuentren fuera de la subregión espacial se obtiene de la siguiente manera: la probabilidad de que las tres moléculas estén fuera es

de modo que la "inesperabilidad" es

Estos cálculos demuestran que es más inesperado el hecho de encontrar las tres moléculas dentro de la subregión, lo que es bastante claro, puesto que es mucho mayor la región exterior y es más factible que allí se encuentren.

Podemos concluir que la medida de lo "inesperado" es una medida de nuestro grado de desinformación.  

Si tenemos dos sucesos independientes, que son excluyentes, con probabilidades 

Figura 1

Figura 2

respectivamente. Cada uno de ellos tendrá su propia "inesperabilidad", y parece claro que la inesperabilidad de que alguno de ellos ocurra (de la unión entre ambos), es la suma de ambas, esto es

       (*)

puesto que la probabilidad conjunta de ambos sucesos (la intersección) es

y el logaritmo natural con signo menos es justamente la expresión (*).

Entropía

Supongamos que tenemos una partición de tamaño N de un espacio de probabilidad, donde cada suceso de la partición tiene probabilidad 

de ocurrir. Entonces definimos la entropía como

Observemos que la entropía es una suerte de valor medio de la "inesperabilidad".

La entropía caracteriza  el grado de indeterminancia o aleatorización que puede ocurrir en una situación dada. En efecto, si observamos con atención la gráfica de la figura 1, podemos notar que mientras mayor probabilidad de ocurrencia de un suceso (grado de certeza) la entropía tenderá a cero; por el contrario, si la probabilidad de ocurrencia es nula, entonces la entropía, la desinformación es alta.

Veamos un ejemplo. Considere una molécula A que se encuentra en un cubo de volumen V, y existe una región fija dentro del cubo de volumen . Entonces la molécula puede estar en el interior de esta última región, con probabilidad o puede estar en el exterior con probabilidad , de modo que su entropía es