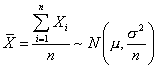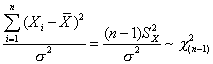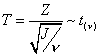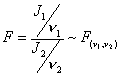|
Estadística inferencial: resultados previos |
||
|
Supongamos que tenemos dos variables aleatorias X e Y,
cada una de ellas con función de densidad f(x) y g(y) respectivamente. Se
puede demostrar que si ambas variables aleatorias son independientes,
entonces la función de densidad conjunta del vector aleatorio (X, Y)
tiene función de densidad (conjunta) f( x, y) = f(x) g(y). Esto es, la
densidad conjunta es el producto de las densidades.
Es saludable recordar (o definir, si no se ha hecho antes) que dos variables aleatorias X e Y son independientes si para cualquier par de intervalos (a, b) y (c, d) (boreleanos en R) las imágenes inversas, esto es X-1{(a, b)} e Y-1{(c, d)} son independientes como sucesos. Ahora, de igual forma como se define cuando una colección finita de sucesos son independientes, podemos definir cuando una colección finita de variables aleatorias, cada una de ellas con función de densidad, son independientes. Diremos que una colección X1, X2, ..., Xn de variables aleatorias, con funciones de densidad f1(x1), f2(x2), ..., fn(xn) respectivamente, serán independientes si para cualquier subcolección {j1,j2,...,jk} de {1, 2, ..., n} la densidad conjunta del vector aleatorio
tiene función de densidad conjunta
Vamos a enunciar algunos resultados fundamentales sobre variables aleatorias independientes en relación con la distribución normal. 1. Si X1, X2, ... , Xn son variables aleatorias independientes, de modo que cada Xi sigue una distribución N(mi, s2i), entonces
2. Si X1, X2, ... , Xn son variables aleatorias independientes, de modo que cada Xi sigue una distribución N(m, s2), entonces
|
3. Si X1, X2, ... , Xn son variables aleatorias independientes, de modo que cada Xi sigue una distribución N(m, s2), y si hacemos las transformaciones
entonces Z1, Z2, ... , Zn son variables normales estándar e independientes, y además
4. Sean X1, X2, ... , Xn variables aleatorias independientes tal que cada Xi sigue una distribución N(m, s2), entonces
además X y S2X son variables aleatorias independientes. 5. Sea Z una variable aleatoria normal estándar y J una variable aleatoria ji-cuadrado con n grados de libertad, y si Z y J son independientes, entonces
donde t(n) es la distribución t-student con n grados de libertad. 6. Sean J1 y J2 dos variables aleatorias independientes que se distribuyen según una ji-cuadrado con n1 y n2 grados de libertad respectivamente, entonces
donde esta distribución se conoce como distribución F de Fisher con n1 grados de libertad en el numerador y n2 grados de libertad en el denominador. |
|