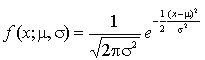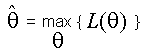|
La función de máxima verosimilitud |
||
|
Supongamos que tenemos una variable aleatoria X,
que caracteriza un atributo que deseamos medir de cierta población, como
por ejemplo la altura de un individuo, o también X puede
representar el largo de un tornillo que fabrica una fábrica de tornillos,
o X puede representar el número de artículos defectuosos que se
pueden obtener de una partida de artículos de fabricación, etcétera.
Vamos a suponer que esta variable aleatoria se rige por una determinada
función de densidad (o cuantía), digamos f(x, q).
Donde q es un
parámetro que define o caracteriza a la función de densidad (o
cuantía). Por ejemplo si la función de densidad es la normal, esto es
entonces el parámetro q es el vector bidimensional q = (m, s) Ahora bien, lo que hemos aprendido en Estadística Descriptiva es obtener varios datos estadísticos, digamos n datos estadísticos, al aplicar n veces, en forma independiente, la variable aleatoria X que mide lo que queremos que mida (la estatura de un pequeño, el largo de un tornillo, o el número de artículos defectuosos de una partida, etcétera). Esta aplicación de n veces la medición X, se denota por (X1, ..., Xn) y que representa el hecho de que "vamos a medir" (una expresión de futuro), y cuya medida de incertidumbre para este "vector aleatorio" está generada por la densidad conjunta f(z1, q) ...f(zn, q) esto es, el producto de la función de densidad f(x, q), n veces. Ahora bien, si "realizadas estas n mediciones" (una expresión de pasado), obtendremos los siguientes datos estadísticos (X1= x1, ..., Xn= x1) y para estos valores, y solo para estos valores, tenemos la función L(q) = f(x1, q) ...f(xn, q) (1) que llamaremos función de verosimilitud. Esta función tiene como variable a q en el dominio en que está definido en la función de densidad original. Insistimos en que los valores x1, x2, ..., xn son valores conocidos. De otra forma si en la ecuación (1) asignamos un valor arbitrario a L(q) existe la posibilidad de "despejar" q en función de los valores x1, x2, ..., xn . Digamos que sería una forma "arbitraria" de encontrar un estimador para el verdadero valor de q. ¿Qué valor "no arbitrario" podríamos asignar a L(q), para tener un estimador de q?. Observemos que la expresión en (1) está indicando el valor de la densidad (conjunta) al obtener una muestra de tamaño n de una variable de X que tiene la densidad f(x; q). A fin de ponernos en todos los escenarios posible (recuerde que no sabemos el valor verdadero de q), podemos exigir a fortiori que L(q) sea máximo, es decir elegir el valor de q de modo que (1) tenga el máximo valor.
|
Se define entonces el estimador máximo verosímil para q,
para los valores obtenidos x1, x2,
..., xn, por
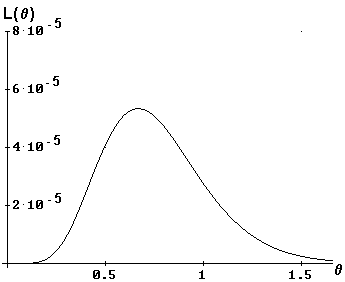
Es claro que este valor dependerá de los valores de x1, x2, ..., xn. Veamos un ejemplo. Supongamos que el tiempo de duración de un artefacto se rige por una densidad exponencial de la forma f(t, a) = ae-at siendo a el parámetro desconocido. Vamos a suponer entonces que seleccionamos al azar 7 de estos artefactos y los hacemos funcionar y anotamos los siete tiempos de duración. Supongamos que estos tiempos de duración son {1.5; 1.7; 1.4; 1.35; 1.45; 1.5; 1.6} De manera que la función de verosimilitud es L(q) = a7e-21a / 2 (2) A efectos didácticos, la gráfica de esta función es
En esta gráfica se puede observar que esta función tiene un máximo. Analíticamente para obtener este máximo debemos derivar la función dada en (2) e igualar a cero, para obtener los "candidatos a máximo (o mínimos)". Esto es d [L(q)] / dq = 7a6 e-21a/2(2-3a) / 2 Si igualamos a cero, y si las soluciones las reemplazamos en la segunda derivada se concluye que el máximo se obtiene en a0 = 2/3 De manera que el estimador máximo verosímil para a es a0 = 2/3. Además notemos para este ejemplo que â es igual al valor recíproco del promedio de los 7 tiempos de la muestra, esto es a0 = (S ti / 7)-1 = (3/2)-1 Lo cual es una coincidencia muy agradable, puesto que sabemos que la esperanza de una variable T que tenga densidad f(t, a) = ae-at es E[T] = 1/a En resumen, si t1, ..., tn es una muestra de tamaño n obtenida de una densidad f(t, a) = ae-at entonces el estimador máximo verosímil para a es a0 = (S ti / n)-1
|
|