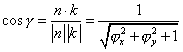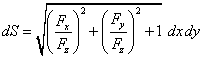(*): Trabajaremos con superficies de tal forma que pueda ser proyectada sobre el plano XY de manera unívoca. Esto es, que toda recta paralela al eje Z corta a la superficie S una sola vez. Si este no es el caso, S puede ser dividida en porciones de tal forma que cada porción tenga esta propiedad, y pueda ser tratada con el método que aquí se entregará.

Existen tres formas de describir una superficie "suave" como la dibujada en la Figura 1.

Una primera forma es mediante la ecuación

z = j ( x, y ) (1)

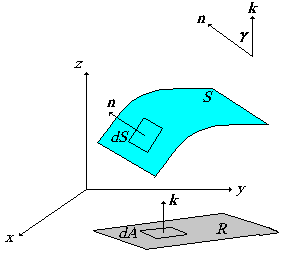
con x e y definidos en alguna región del plano. En rigor, en este caso, la región será la proyección de esta superficie sobre el plano XY. Observe la Figura 2, donde se muestra la proyección de la superficie S, que denotaremos por R, sobre el plano XY.

Nuestro interés es calcular una expresión para un elemento de superficie infinitesimal, que llamaremos dS, y cuya proyección sobre el plano XY forma un elemento de área dA = dx dy, como lo indica la Figura 3.

Figura 1.

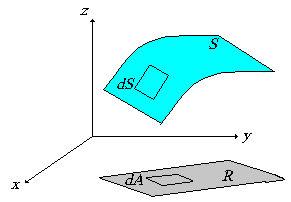
Figura 3

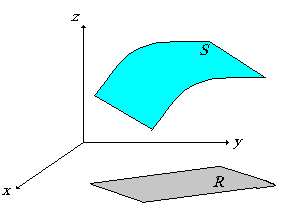
Figura 2

En primer lugar notemos que un vector normal (unitario) al elemento de área dA es el versor k. Vamos a obtener ahora un vector normal al elemento de superficie dS. Notemos que de la ecuación 1, se tiene que

de manera que obtenemos la ecuación

Y esto significa que el vector

es perpendicular a todo vector infinitesimal dx i + dy j + dz k que está en la superficie S, y en consecuencia n es un vector normal a la superficie. La relación entre los vectores normales a dS y dA, respectivamente, como lo son n y k, se muestra en la Figura 4.

Podemos observar que el ángulo g entre ambos vectores normales, es el mismo ángulo que existe entre los elementos dS y dA, esto es dA = cos g dS. Y sabemos que cos g lo podemos calcular mediante

de modo que

Fórmula que nos entrega el cálculo el área del elemento infinitesimal dS.

La otra forma en que se puede entregar una superficie es

Figura 4

F(x, y, z ) = 0, llamada en su forma implícita. En este caso tenemos la ecuación

Lo que se deduce que el vector

es perpendicular a cualquier vector infinitesimal dx i + dy j + dz k que está en la superficie S. Y en consecuencia, esta vez, trabajando de manera análoga obtenemos la relación

Teoría de superficies *: algunos conceptos