| Hasta el momento hemos estudiado superficies en su forma
cartesiana, esto es z = j (x, y),
o en su forma cartesiana implícita, esto es F( x, y,
z) = 0. Sin embargo, es frecuente representar a una superficie en
su forma paramétrica. Se necesitan dos parámetros para describir los
puntos cartesianos y en consecuencia tener la descripción de la
superficie, esto es |
|
x = x( u, v ) ; y
= y(u, v ) ; z = z( u, v)
(1)
|
|
donde u y v son dos parámetros (variables) independientes
y están definidos en algún dominio de R2.
|
|
El ejemplo más trivial resulta de la representación paramétrica de
una porción de esfera (o de la esfera completa). Figura 1
|
| En este caso se tiene |
|
x = a sen f
cos q ; y = a
sen f sen q
; z = a cos f |
| De la forma paramétrica general dada en
(1), a veces resulta sencillo eliminar los parámetros u
y v, y llegar a la forma F( x, y,
z) = 0 |
| En cualquier caso, obtenida la forma
paramétrica (1), podemos definir el vector posición
que determina cualquier punto de la superficie. Este
vector posición está dado por |
|
r( u, v )
= x( u, v ) i + y(u,
v ) j + z( u, v) k |
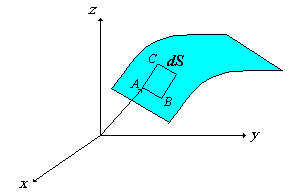
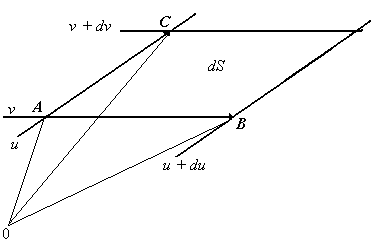
| Mediante este vector posición podemos
determinar el valor del área de una superficie
elemental infinitesimal. |
|
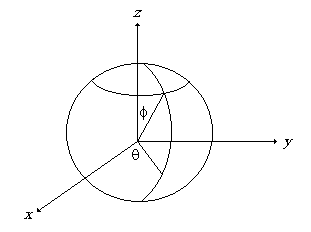
Figura 1 |
|