| En la sección vamos a analizar el comportamiento de un campo escalar de dos variables del tipo f(x, y) al efectuar un cambio de variable del tipo x = x(r, q), y = y(r, q) y la incidencia que tendrá en el gradiente Ñf. Este desarrollo se puede generalizar a tres o más variables. |
| El gradiente para el campo escalar f(x, y) está dado por |
|
|
| Por otro lado, si tenemos un cambio de variable "bueno" de la forma x = x(r, q), y = y(r, q), entonces esencialmente se tiene que f(x, y) = f(x(r, q), y(r, q)) = f(r, q), y en consecuencia la interrogante es ¿cómo será el gradiente del campo escalar en estas nuevas variables? |
|
La diferencial para f(x, y) está dada por |
|
|
| y la diferencial para f(r, q) estará dada por |
|
|
| Es claro que en cualquier caso df(x, y) = df(r, q). Ahora, en virtud de que x = x(r, q), y = y(r, q) podemos calcular las diferenciales dx y dy, esto es |
|
|
| Reemplazando estas últimas ecuaciones en (1), obtenemos |
|
|
| Y, en consecuencia, comparando las expresiones en (2) y (4), podemos concluir la versión bidimensional de la regla de la cadena, esto es |
|
|
| Con esto hemos calculado el diferencial de f en las nuevas variables r y q. Vamos ahora al cálculo del gradiente en estas nuevas variables. |
| De la expresión (5) podemos calcular las derivadas parciales de f en las variables x e y . En efecto, matricialmente las ecuaciones en (5) se pueden expresar como |
|
|
| Este sistema tiene una única solución si el determinante de la matriz de 2 x 2 es distinta de cero (y esta es nuestra exigencia al decir que tenemos un cambio de variable "bueno"). Despejando obtenemos |
|
|
| Para fijar ideas, y no hacer demasiada abstracción, trabajemos con el siguiente cambio de variables (coordenadas polares) |
|
|
| de modo que el sistema en (6) queda como |
|
|
| y cuya solución es |
|
|
| Entonces reemplazando estos valores en la fórmula del gradiente de f dada en (0), obtenemos |
|
|
| Trabajando algebraicamente, |
|
|
| Hagamos |
|
|
| que claramente son vectores unitarios. Es decir |
|
|
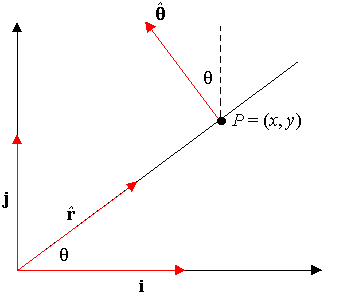
| Estos nuevos vectores (que son ortogonales) tienen una sencilla interpretación como se puede observar en la siguiente figura, |
|
|
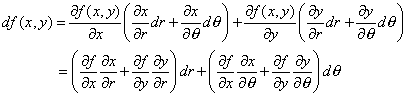 (4)
(4)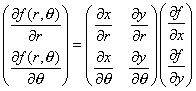
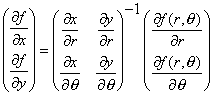 (6)
(6)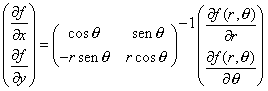
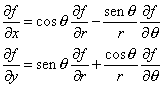 (7)
(7)