La interpretación física de la expresión (2) es trivial, es simplemente la diferencia (crecimiento o decrecimiento) entre las mediciones que otorga la función j en los puntos P₀ y P. Pensemos por ejemplo que j mide la temperatura en los puntos de una región del espacio, luego j ( P ) - j ( P₀ ) es simplemente la diferencia de temperatura entre los puntos P y P₀.

Ahora bien, es claro cuando P se aproxime a P₀ esta diferencia se irá aproximando a cero (entendiendo que P y P₀ están dentro de una región donde está bien definida la función j).

Ahora bien, lo que vamos a "exigir" de esta diferencia que se aproximará a cero (en cuanto P se aproxime a P₀) es que sea "muy suave", "muy buena", que ojalá la aproximación sea mediante un plano. Si esto ocurre, diremos que el campo escalar j es diferenciable en el punto P₀. ¿Qué entenderemos matemáticamente por aproximación buena? es decir ¿que entenderemos por j es diferenciable en el punto P₀? Lo siguiente: j es diferenciable en el punto P₀ si existen tres números reales A, B y C y una función real de tres variables h tal que se satisfaga lo siguiente,

j (a + h, b + k, c + l) = j (a , b, c) + Ah + Bk + Cl + h (h, k, l) (3)

de tal manera que

(4)

La exigencia en (4) nos dice que la función h (h, k, l) es tan "despreciable" que cuando (h, k, l) se aproxima al (0, 0, 0) entonces h (h, k, l) se aproxima al cero (y se aproxima muy rápido al cero, que incluso dividiéndolo por la norma de (h, k, l), que hemos denotado por l, igual se aproxima al cero).

La expresión en (3) nos dice entonces que cuando (h, k, l) está muy cerca del (0, 0, 0), o, que es lo mismo, cuando P está muy cerca de P₀, entonces

(5)

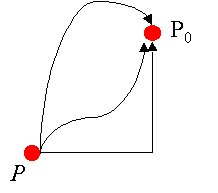
Una observación muy importante: La aproximación desde P hasta P₀ es cualquier aproximación. Observe la Figura 1, en ella se muestran varias formas de aproximarse a P₀ desde P.

Esto significa que si j es diferenciable en P₀, entonces no importando la trayectoria con que P se aproxime a P₀, los valores de A, B y C son independientes de estas trayectorias. Esto nos ayudará para encontrar los valores de A, B y C. En efecto, Sea P = (a + h, b, c) Es decir, nos aproximaremos a P₀ = (a, b, c) en la dirección dada por el versor i, observe la Figura 2, de tal forma que la expresión (5) queda,

dividiendo por h y tomando límite cuando h tiende a cero,

(6)

Figura 1

En efecto, resulta ser que el valor de A es simplemente la derivada parcial de j respecto de la primera componente. Para la aproximación (a , b + k, c) hacia (a, b, c), obtenemos

(7)

Y mediante (a , b, c + l) hacia (a, b, c), obtenemos

(8)

Figura 2

(6), (7) y (8) reemplazando en (5) obtenemos

En general, si j es diferenciable en cualquier punto de una cierta región, entonces para cualquier punto (x, y, z) de esa región

de tal forma que para Dx, Dy, Dz infinitesimal, obtenemos la diferencial dada inicialmente en (1)

En rigor, esta última expresión está escrita como un operador, es decir este operador tiene una expresión toda vez que se aplique a un punto. Veamos un ejemplo.

Ejemplo. Sea j (x, y, z) = x y²z², y queremos calcular la diferencial en el punto (1, 1, 1). Calculamos las derivadas parciales del campo escalar y evaluamos en el punto (1, 1, 1). Esto es

y evaluando estas derivadas parciales en (1, 1, 1) obtenemos la diferencial,

(9)

Muy bien, pero ¿qué significa esta expresión? o ¿qué utilidad presta?

En primer lugar, dj (1, 1, 1) está midiendo el diferencial de cualquier valor infinitesimalmente próximo al valor (1, 1, 1), y consagra como vector diferencia entre el punto (1, 1, 1) y cualquier otro punto infinitesimalmente próximo al vector

dx i + dy j + dz k = dr

Observemos la Figura3.

La diferencial en (9) se puede expresar como

(10)

Calculemos la magnitud del vector dr, y denotémosla por

dividiendo por ds la expresión en (10), obtenemos

donde el vector dr/ds es unitario.

Figura 3

Diferencial de un campo escalar