| Entenderemos, de momento, por campo vectorial como una función vectorial definida sobre los puntos (o una región) en el espacio físico (en R3). De otra forma, la función vectorial F(x, y, z) es un campo vectorial si existen tres funciones escalares con dominios en (o en una región de) R3, digamos F1(x, y, z), F2(x, y, z) y F3(x, y, z) donde |
|
F(x, y, z) = F1(x, y, z) i + F2(x, y, z) j + F3(x, y, z) k |
| Existen variados ejemplos de aplicaciones en la física, aunque rigurosamente hablando, podemos decir que es la física que hace fecunda y da acta de nacimiento al cálculo vectorial o análisis en campos vectoriales. Solo para citar el ejemplo más trivial, consideremos la velocidad de un cuerpo que se mueve en el espacio, y queremos determinar la velocidad de este cuerpo, que es un vector, cuando el cuerpo se encuentra en la posición (x, y, z). Aunque en rigor, esta velocidad eventualmente puede depender del tiempo t tanto como de la posición. Si este es el caso, se tendría un campo vectorial de velocidad de la forma v = v(x, y, z, t) = v1(x, y, z, t) i + v2(x, y, z, t) j + v3(x, y, z, t) k. En el caso de que el campo no dependa del tiempo se habla de campo vectorial "estable" (steady), en oposición a "inestable" (unsteady) |
| Tanto la diferenciación como la integración de funciones vectoriales (campos vectoriales) siempre se pueden desarrollar mediante un tratamiento separado en sus componentes, y puesto que cada componente es un campo escalar, sobre estas se aplican todas las técnicas desarrolladas en las secciones anteriores. De modo que simplemente anunciaremos que |
|
|
| Sea j un campo escalar, entonces el gradiente de este campo escalar define un campo vectorial F, en efecto |
|
|
| La pregunta que surge es la inversa. dado un campo vectorial F, ¿existe un campo escalar j tal que (1) se cumple? La respuesta es "no siempre", o para ser más preciso "es la excepción más que la regla de que la respuesta sea positiva". |
| Como quiera que sea, supongamos por un momento de que dado un campo vectorial F existe un campo escalar j tal que se cumple que |
|
|
| Consideremos la superficie definida por todos los puntos (x, y, z) tales que j(x, y, z) = constante. Sobre esta superficie se tiene que |
|
|
| Por otro lado, sea dr = dx i + dy j + dz k un vector infinitesimal que pertenece a dicha superficie, entonces |
|
|
| Reemplazando (2) en esta última igualdad nos queda |
|
|
| Entonces podemos concluir que F, por (2), es la máxima derivada direccional de j, y además, por (3), el campo vectorial F y el elemento dr de la superficie son perpendiculares. |
| Finalmente, si ocurre (2), entonces el campo vectorial F se dice que es conservativo y j es el potencial para el campo. De modo que todo campo vectorial conservativo es normal a las superficies de nivel de su potencial. |
| Ejemplo. Consideremos la fuerza gravitacional, dada por |
|
|
| que actúa conforme se detalla en la Figura 1. El vector r está orientado desde el origen, donde se encuentra el cuerpo de masa M, hacia la posición donde se encuentra el cuerpo de masa m, donde r = x i + y j + z k., de modo que (4) es equivalente a |
|
|
| Sea el siguiente campo escalar |
|
|
| No resulta para nada complicado verificar que el gradiente es este campo escalar es precisamente F, esto es se cumple que |
|
|
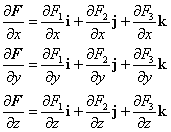
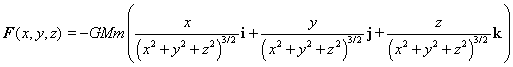 (5)
(5)