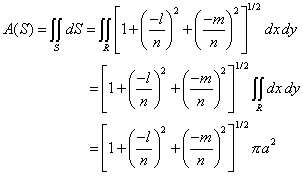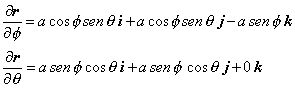| Ahora que hemos encontrado una expresión para el elemento de superficie infinitesimal dS, que consiste en buscar su relación sobre un plano de proyección (nosotros hemos proyectado la superficie sobre el plano XY, pero perfectamente podía haber proyectado la superficie sobre el plano XZ, o el plano ZY, eso dependerá de cuál proyección nos entrega una integral más sencilla). De esta forma el área de una superficie (suave), A( S ), está dada por |
|
|
| si la superficie S está dada por z = j( x, y). |
| En el caso de que la superficie esté en forma paramétrica, esto es |
|
r( u, v ) = x( u, v ) i + y(u, v ) j + z( u, v) k |
| entonces el área de la superficie está dada por |
|
|
| siendo D el dominio de definición de los parámetros (u, v). |
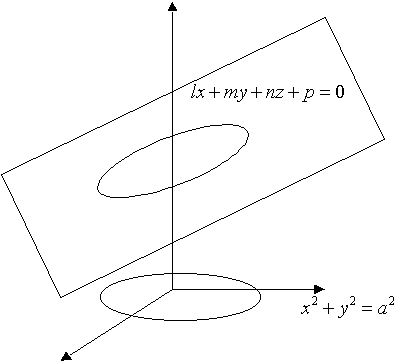
| Ejemplo 1. Encontrar el área de la porción del plano lx +my + nz + p = 0 que está en el interior del cilindro x2 + y2 = a2. Figura 1. |
|
|
| Proyectaremos la porción del plano sobre el plano XY. Por otro lado, la superficie del plano está determinada por |
|
z = j( x, y ) = - ( lx + my + p ) / n |
| de tal forma que |
|
|
| Aplicando la fórmula (1), nos queda |
|
|
| puesto que la última integral es simplemente el área de la circunferencia x2 + y2 = a2, que es pa2. |
| Ejemplo 2. Encontrar el área de superficie de una esfera de radio a. |
| Sabemos que una la superficie de una esfera de radio a se puede describir mediante coordenadas esféricas, esto es |
|
x = a sen f cos q ; y = a sen f sen q ; z = a cos f |
| es decir |
|
r( j, q ) = a sen f cos q i + a sen f sen q j + a cos f k |
| con |
|
|
| y puesto que |
|
|
| Entonces |
|
|
| Aplicando la fórmula (2), nos queda |
|
|
 Figura
1
Figura
1