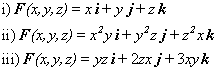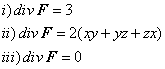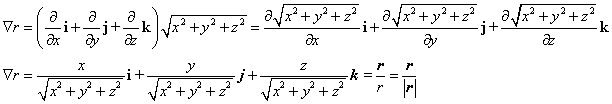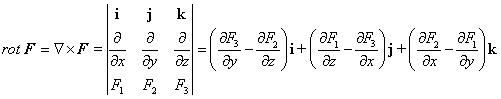| Hemos visto como el gradiente de un campo escalar j
define un campo vectorial, esto es |
|
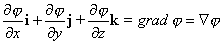
|
| La expresión Ñj nos indica
la idea de una cierta multiplicación ordinaria entre el "elemento Ñ"
y la función j, de modo que vamos a definir
el operador Ñ como |
|
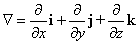
|
| el cual ciertamente no es un "vector" en el
sentido estricto, aún cuando tiene soporte en en los versores
canónicos. Supongamos que, para operar, a Ñ
lo vamos a considerar como un (seudo) vector, de modo que si tenemos,
por ejemplo, un cierto campo escalar F(x, y,
z) = F1(x, y, z) i
+ F2(x, y, z) j + F3(x,
y, z) k entonces tiene sentido el siguiente
producto punto |
|
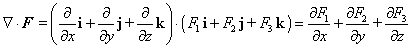
|
| y vemos que la resultante es un campo escalar. Definimos
a este especial producto punto entre el operador Ñ y el campo escalar F(x,
y, z) como la divergencia, y se denota como |
|
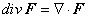
|
| Es claro que esta definición operacional tendrá una
relevante importancia física que veremos más adelante (algo
anunciamos, la divergencia de un campo vectorial será un límite del
flujo del campo por unidad de volumen). Sin embargo en esta sección
estaremos más interesados en la operatoria matemática más que en su
interpretación física. |
| Ejemplo. Para los siguientes campos vectoriales
calculas la divergencia, |
|
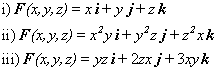
|
| Las respuestas son |
|
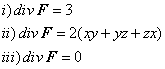
|
|
| Nos vamos a detener un momento en el ejercicio ( i )
anterior para precisar algunos conceptos notacionales. Considerando el
campo vectorial r = x i + y j + z
k, tenemos que existe un campo escalar trivial asociado a este, a
saber |
|
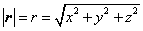
|
| de modo que el operador Ñ
puede actuar sobre estos dos campos, a saber |
|
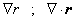
|
| donde |
|
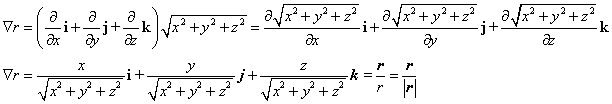
|
| mientras que |
|
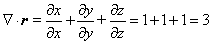
|
|
| Existe otra operatoria notable que podemos definir entre
el (seudo) vector Ñ y un campo vectorial F,
a saber |
|
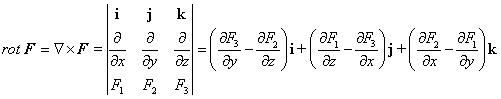
|
| y que llamaremos rotor del campo F. Como
antes, este campo vectorial tiene una interpretación física que luego
veremos, por ahora estaremos interesados en su operatoria matemática. |
| Ejemplo. Calcular el rotor del campo F(x,
y, z) = x i + y j
+ z k. Se tiene que rot F = 0 |
|
| Hemos dicho que el operador Ñ
se puede tratar como un (seudo) vector, entonces bajo esta óptica tiene
sentido la expresión Ñ2, esto es |
|
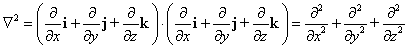
|
| y si j es un campo escalar,
entonces |
|
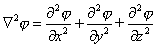
|
| Y si tenemos el campo vectorial F(x,
y, z) = F1(x, y, z)
i + F2(x, y, z) j +
F3(x, y, z) k, también
tiene sentido Ñ2F,
esto es |
|
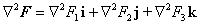
|