|
Henos establecido que para la curva r( t ) = x(
t ) i + y( t ) j + z( t
) k existen dos vectores unitarios y ortogonales entre si, a
saber |
|
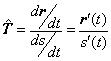 (1)
(1)
|
|
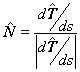 (2)
(2)
|
|
donde |
|
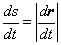
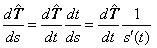
|
|
Con estos vectores unitarios, podemos definir un nuevo vector unitario y
ortogonal a ambos, |
|
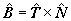
|
|
A este vector se le conoce como vector binormal. De tal forma que, para
un punto cualquiera de la curva, se asocian tres vectores ortogonales
unitarios que forman un sistema de orientación positiva, como lo indica
la Figura 1. |
| Notemos que si r( t
) = x( t ) i + y( t
) j + z( t ) k describe la
posición de una partícula, entonces sabemos que la
velocidad y la aceleración de la partícula están
dadas, respectivamente, por |
|
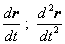
|
| y se puede ver que estos vectores tienen
la misma dirección que los vectores tangente y normal,
respectivamente. |
| La curva de la Figura 1 está modelada
por la función |
|
r( t ) = cos(2 t
) i + sen( 2t ) j + 2 t
k |
| No resulta complicado deducir que los
vectores unitarios asociados a cada punto de esta curva
son |
|
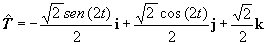
|
|
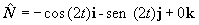
|
|
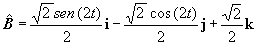
|
|
|
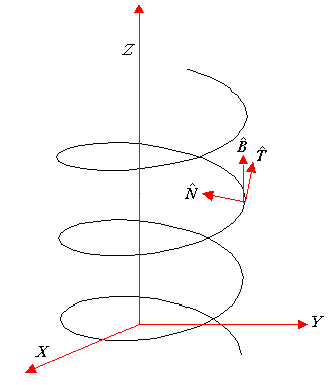
Figura 1 |
|
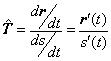 (1)
(1)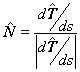 (2)
(2)