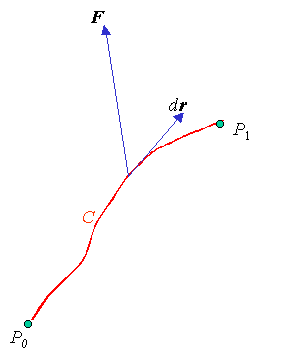
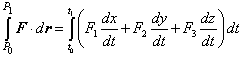| de modo que el trabajo total realizado por la fuerza F
moviéndose desde P0
hasta P1 a lo largo de la curva C es
la suma de todas estas contribuciones infinitesimales, esto es la
integral dada en (1) |
|
| Ahora daremos los pasos analíticos para evaluar una
integral de línea de un campo vectorial definido sobre una curva C. |
| En primer lugar, debemos encontrar una ecuación
paramétrica para la curva (no necesariamente definirla mediante el
parámetro natural s, longitud de arco). Supongamos que tenemos
una representación paramétrica r = r( t
), donde los valores t = t0 y t = t1
corresponden a los puntos P0 y P1.
Entonces la primera integral de (1) puede escribirse como |
|
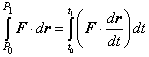 (2)
(2)
|
| donde la integral de la derecha es una integral ordinaria
en una variable. El producto punto de la función que se integra puede
desarrollarse de la siguiente manera. Sea el campo vectorial |
|
F = F1( x, y,
z ) i + F2( x, y, z
) j + F3( x, y, z ) k |
| y el vector r que describe la curva en
su forma paramétrica |
|
r( t ) = x( t ) i
+ y( t ) j + z( t ) k |
| entonces |
|
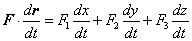
|
| Reemplazando esta expresión en (2), nos queda |
|
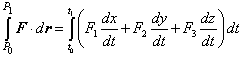
|
| Y esta integral, por lo general (salvo que el profesor
diga lo contrario), es una sencilla integral
ordinaria de una sola variable. Sin embargo hay que tener cuidado con
esta fórmula. El resultado no sólo dependerá de los
puntos P0 y P1, sino que también
dependerá, en general, del camino C que conecta ambos puntos. |
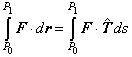 (1)
(1)
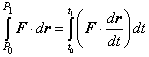 (2)
(2)