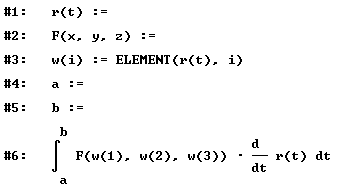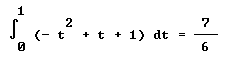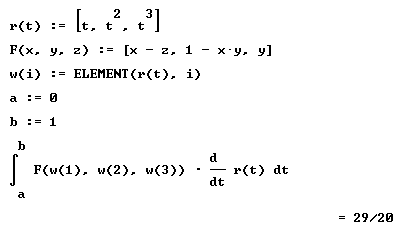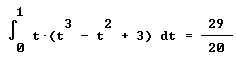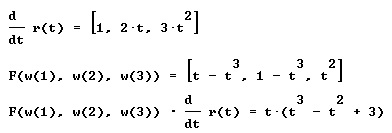| Daremos dos ejemplos para calcular una integral de línea sobre un mismo campo vectorial. Queremos calcular la integral |
|
|
| donde F( x, y, z ) = ( x - z ) i + (1 - xy ) j + y k, y C es la curva determinada por: |
| ( i ) el segmento de recta que une los puntos (0, 0, 0) y (1, 1, 0) |
| ( ii ) x = t ; y = t2 ; z = t3 que une los puntos (0, 0, 0) y (1, 1, 1) |
|
La resolución de este problema de cálculo la realizaremos con ayuda de un sencillo programa realizado en el DERIVE, que además de simplificar el tiempo de cómputo, es bastante didáctico en los pasos a seguir para obtener el resultado de la integral pedida. |
| Escriba en el software DERIVE lo siguiente (si no tiene el software, o no tiene interés en utilizarlo, siga con lápiz y papel los pasos indicados): |
|
|
|
La instrucción nº 1 dice que se debe escribir la ecuación paramétrica de la curva, en nuestro caso, si queremos resolver la parte ( i ) del problema, esto es la recta que une los puntos puntos (0, 0, 0) y (1, 1, 0), entonces escribimos |
|
|
| Observe (para los que usan el DERIVE) como deben escribir la función vectorial, con "paréntesis cuadrados". |
| La instrucción nº 2 dice que se debe escribir el campo vectorial. En nuestro ejemplo debemos escribir |
|
|
| Nuevamente, para los que usan el DERIVE, la función vectorial se debe escribir con "paréntesis cuadrados". |
| La instrucción nº 3, establece las componentes cartesianas de la curva, puesto que será utilizada posteriormente para definir el campo vectorial sobre dicha curva. El software DERIVE internamente asigna que w( 1 ) será igual a la primera componente de la forma paramétrica de la curva r( t ); w( 2 ) y w( 3 ) asumen como valores la segunda y tercera componente de la ecuación paramétrica de la curva, respectivamente. |
| las instrucciones nº 4 y nº 5 dicen que deben definirse los valores de a y b que son los correspondientes a los puntos (0,0,0) y (1, 1, 0), respectivamente, de otra forma a y b deben ser tales que r( a ) = (0, 0, 0) y r( b ) = (1, 1, 0). En nuestro caso, se tiene que |
|
|
| Y finalmente, en la instrucción nº 6, aquellos que están utilizando el DERIVE, deben posicionarse con el cursor en la instrucción, y luego buscar un icono con el signo igual y hacer click, y esperar el resultado. (Los que no usan el DERIVE, deben con el lápiz calcular la derivada de r( t ), luego calcular el campo vectorial aplicado a la curva, luego realizar el producto punto entre este campo vectorial y la derivada de r( t ), y luego integrar respecto de t entre los valores de a y b. No queda más que desearles mucha suerte en esa aventura). |
| El resultado debe ser (para los que usan el lápiz): |
|
|
| Para el caso ( ii ), lo resolvemos de igual forma, el proceso es (con o sin lápiz): |
|
|
| es decir |
|
|
| En efecto, puesto que |
|
|