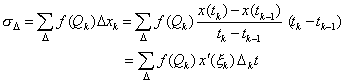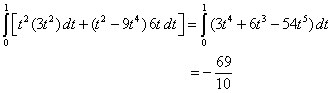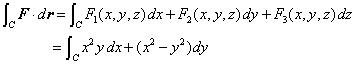| Consideremos la curva r( t ) = x( t ) i + y( t ) j + z( t ) k, y supongamos que está definida en un intervalo [a, b], y supongamos además que existe la derivada de r( t ) y además su derivada es no nula en dicho intervalo (en este caso se dice que la curva es suave en dicho intervalo). Denotemos a la curva definida por r( t ) como C. |
| Sea f una función con valores reales definida sobre la curva C. Vamos a definir lo que entenderemos por la integral de línea de f sobre C. |
| Supongamos que en el intervalo [a, b] realizamos una partición que llamaremos D, |
|
D : a = t0 < t1 < ... < tn = b |
| Esta partición induce a una partición en la curva en los siguientes puntos |
|
P0 = r( t0), P1 = r( t1 ), ... , Pn = r( tn ) |
| Ahora bien, en cada intervalo [tm-1, tm] seleccionemos un elemento arbitrario tm y definamos Qk = r( tm ). Formemos ahora la suma |
|
|
| donde Dxk = xk - xk-1. Ahora si el siguiente límite existe |
|
|
| entonces su valor se denotará por |
|
|
| Definiciones similares se obtienen para las integrales |
|
|
| El desarrollo analítico de las integrales (1) y (2) las entrega el siguiente teorema |
| Teorema. Si C es una curva suave definida por r( t ) = x( t ) i + y( t ) j + z( t ) k , con t en el intervalo [a, b], entonces |
|
|
| Demostración. (Esbozo) Para toda partición D se tiene que |
|
|
| donde en la última igualdad hemos aplicado el teorema del valor medio, con xk entre [tk-1, tk] y Qk = r( xk ). Y esta expresión es la aproximación de una derivada simple real, de modo que aplicando el límite a la partición D, esto es cuando D tiende a cero, obtenemos el resultado. |
| Ejercicio. Calcular la siguiente integral de línea |
|
|
| donde C es el arco de curva definido por y = 3x2 desde (0, 0) hasta (1, 3). |
| Solución. La curva la parametrizamos de manera trivial, esto es r( t ) = x( t ) i + y( t ) j, con |
|
x( t ) = t ; y( t ) = 3t2 con t en [0, 1] |
| de este modo la integral de línea en (3) se transforma en |
|
|
| Este ejercicio nos puede sugerir lo que vendrá en la próxima sección sobre integrales de línea. Consideremos el siguiente campo vectorial |
|
F( x, y, z ) = x2y i + (x2 - y2) j + 0 k |
| y consideremos el vector posición usual, esto es r( t ) = x( t ) i + y( t ) j + z( t ) k |
| Entonces la integral en (3), se puede obtener mediante |
|
|