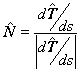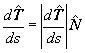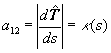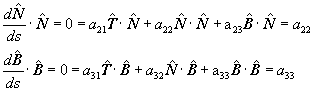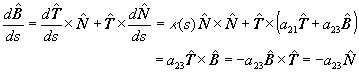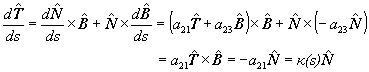|
En la sección anterior establecimos que los vectores unitarios
tangente, normal y binormal que son ortogonales entre sí constituyen
una base vectorial. Consideremos los siguientes vectores |
|
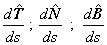 (1)
(1)
|
|
que representan las derivadas respecto de la variable longitud de arco.
Cada uno de estos vectores satisface lo siguiente |
|
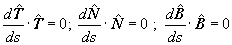 (2)
(2)
|
|
puesto que |
|
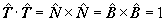
|
|
Por otro lado, cada uno de estos vectores en (1) deben ser combinación
lineal de la base (base que a menudo se llama triedro de Frenet), esto es |
|
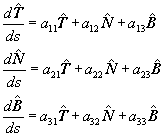 (3)
(3)
|
|
A partir de estas hipótesis vamos a probar las llamadas fórmulas de
Frenet, que son las siguientes |
|
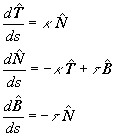 (4)
(4)
|
|
donde los valores k y t
son funciones del parámetro s. |
|
Veamos la demostración de las fórmulas en (4), que no es nada más que
encontrar los valores de aij del sistema de ecuaciones
en (3). |
|
Sabemos que |
|
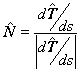
|
|
es decir |
|
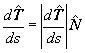
|
|
lo que se deduce, observando la primera ecuación de (3), que a11 = a13 = 0,
y además |
|
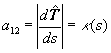
|
|
A este coeficiente le llamaremos coeficiente de curvatura
o simplemente curvatura. De tal modo que |
|
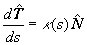
|
|
Ahora vamos a demostrar las dos últimas fórmulas de (4).
|
|
Multipliquemos por el producto punto las dos últimas ecuaciones de (4)
por el vector normal y binormal, respectivamente. Obtenemos que
|
|
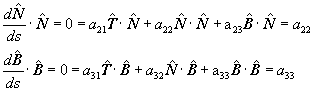
|
|
de modo que a22 = a33 = 0. Ahora
derivemos respecto de s la igualdad
|
|
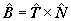
|
|
y obtenemos
|
|
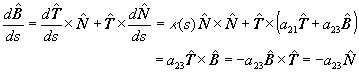
|
|
Al coeficiente a23 le llamaremos coeficiente de
torsión y lo denotaremos por a23 = t(
s ), y de paso, en virtud de la tercera ecuación en (3), hemos
encontrado que a31 = 0 y a32 = - a23
= -t( s ). Con esto hemos demostrado la
tercera fórmula de Frenet.
|
|
Notemos que solo nos falta determinar el coeficiente a21.
Vamos a derivar respecto de s la igualdad
|
|
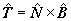
|
|
entonces
|
|
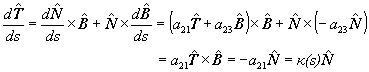
|
|
Por lo tanto a21 = - k( s
). De tal modo que, en virtud de la segunda ecuación de (3), nos queda
que
|
|
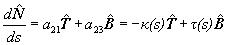
|
|
y con esto hemos demostrado la segunda fórmula de Frenet.
|
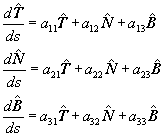 (3)
(3)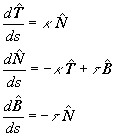 (4)
(4)