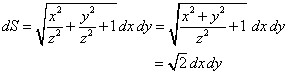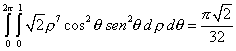La integral para el cálculo del área de una superficie lo podemos extender para una integral de un campo escalar f(x, y, z) definida sobre una superficie S, dada por z = j( x, y ). En efecto, si la superficie S se proyecta sobre una región R en el plano XY (o cualquier otro plano, con los cambios naturales), entonces

donde recordemos que

donde

es el vector unitario normal a la superficie S, y además dA = dx dy

Ahora si la superficie S está en su forma paramétrica, esto es r(u, v) = x(u, v) i + y(u, v) j + z(u, v) k, donde . Y si f(x, y, z) es un campo escalar definido sobre la superficie, entonces

Ejemplo. Se pide evaluar la integral

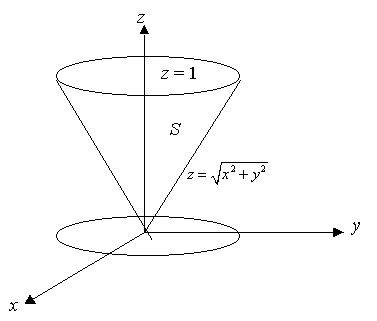
donde S es le superficie lateral del cono x² + y² = z² que yace entre los planos z = 0 y z = 1. Como lo indica la Figura 1.

Proyectando la superficie sobre el plano XY, y considerando que la superficie está entregada en su forma implícita, esto es x² + y² - z² = 0, esto es

F( x, y, z ) = x² + y² - z² = 0

entonces aplicando la fórmula

tenemos que

De modo que debemos integrar

Figura 1

siendo R la región del interior de la circunferencia x² + y² = 1. Esta integral la podemos desarrollar utilizando el cambio de variable a coordenadas polares, esto es

x = r cos q ; y = r sen q

donde dx dy = r dr dq. Entonces la integral nos queda como

Y esta doble integral vale

Ejemplo 2. Este ejemplo nos advierte que la proyección de la superficie debe hacerse en forma conveniente. Evaluar la integral

donde S es la superficie de la semiesfera x² + y² + z² = 1, y > 0

Si proyectamos sobre el plano XY deberíamos efectuar dos proyecciones, una para el hemisferio superior y otra para el inferior. Sin embargo, si proyectamos sobre el plano XZ, obtenemos como región de proyección el interior del círculo z² + x² = 1, y = 0 (R_zx).

En este caso, el elemento de superficie dS estará dado por

donde

Figura 2

Integrales de superficie de un campo escalar