| El objetivo de esta sección es explicar la integral |
|
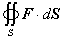 (1)
(1)
|
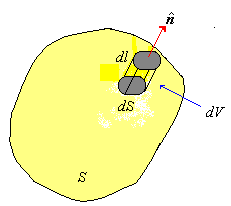
| donde F es un campo vectorial, S es
una superficie suave cerrada, dS es el elemento vectorial
del área de superficie elemental, esto es |
|
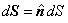
|
siendo 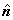 el vector normal unitario a la superficie. Y desde ya, en base a la
explicación que daremos a continuación, la integral dada en (1)
diremos que es el flujo del campo vectorial a través de la superficie.
el vector normal unitario a la superficie. Y desde ya, en base a la
explicación que daremos a continuación, la integral dada en (1)
diremos que es el flujo del campo vectorial a través de la superficie. |
| Flujo, de manera general, es "cantidad" que
fluye por unidad de tiempo (en un lugar especificado). Por ejemplo en un
río, respecto de un punto referencial en una orilla del río podemos
decir que el flujo es de 3 m3/seg. En general,
todo fluido fluye. Y valga la redundancia, puesto que hay
elementos que no son fluidos, en el sentido estricto físico, pero sin
embargo fluye, como por ejemplo el dinero. En efecto, podemos hablar del
flujo de exportación, al decir 5 millones de dólares al mes en flujo
de exportación. Como se quiera, queremos establecer que, por lo
general, el flujo de una cantidad, en un determinado lugar del espacio,
es la variación respecto del tiempo. (Recordemos que el término usado
por Newton para introducir el concepto de derivada fue de fluctuaciones
o flujo). |
| De manera que cuando queremos medir flujo de algo,
debemos establecer en primer lugar el sitio donde vamos a contar el
flujo, el sitio donde pasará el material o el fluido. Pensemos entonces
en una superficie cerrada (que puede ser virtual) |
| Consideremos entonces un fluido que fluye
a través de una superficie cerrada S. |
| Sea v la velocidad del
fluido, y r la densidad del
fluido, que puede variar en cada punto del espacio, y
eventualmente puede varias respecto del tiempo, esto es |
|
v = v( x,
y, z, t ) ; r
= r( x, y, z,
t ) |
| El flujo que pasa a través de la
superficie S se determina primero examinando el
flujo de salida a través de un elemento de superficie dS. |
Notemos que la magnitud de la velocidad
del fluido que pasa por el elemento dS en
dirección 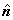 está
dado por está
dado por |
|
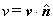
|
| En un tiempo infinitesimal dt
el fluido que pasa a través de dS a la velocidad
v recorrerá una distancia dl. Esto es |
|
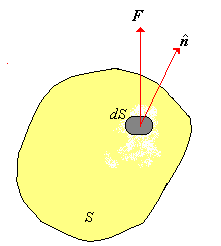
Figura 1 |
|