Gradiente de un campo escalar

En la sección anterior le dimos un sentido a la diferencial total de un campo escalar j, esto es

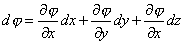
Observemos que, la expresión anterior se puede expresar como el siguiente producto punto

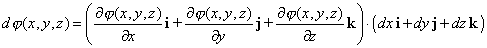(1)

En forma más compacta si denotamos por

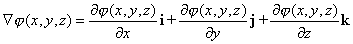(2)

y le llamamos gradiente de j evaluado en el punto (x, y, z), o simplemente gradiente de j si está bajo contexto el punto de evaluación. Y si dr = dx i + dy j + dz k, entonces la expresión (1) queda en forma más compacta como

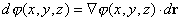(3)

Vamos a introducir el concepto de derivada direccional. De la expresión (3), dividamos por la norma del vector dr, norma que llamaremos ds, entonces

Hagamos u = dr / ds, entonces

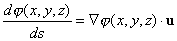(4)

Y esta expresión nos indica la derivada de j en el punto (x, y, z) en la dirección del vector unitario u. Si q es el ángulo comprendido entre el vector gradiente y el vector unitario, entonces de (4) obtenemos

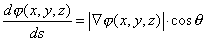(5)

Y la expresión (5) nos indica que el valor máximo que puede tomar la derivada direccional en el punto (x, y, z) es en la dirección indicada por el gradiente, es decir cuando q = 0, y en este caso

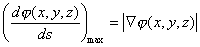(6)

Ejemplo. Encontrar la derivada direccional de la función j (x, y, z) = (x - 1)² +2(y + 1)² + 3(z - 2)² - 6 en el punto (2, 0, 1) en la dirección del vector i -2j - 2k.

Calculando el gradiente de j,

de manera que evaluando el gradiente en el punto (2, 0, 1) obtenemos

Ahora calculando el vector unitario en la dirección indicada,

de modo que

Por otro lado, si hubiésemos considerado la dirección indicada por el gradiente, entonces

Una observación para esta sección. Supongamos que tenemos el campo escalar j (x, y, z), y consideramos la superficie j(x, y, z) = c. Entonces sobre el dominio definido por los puntos que pertenecen a esta superficie la función diferencial es cero, es decir dj (x, y, z) = 0. Esto es

(7)

Y esta ecuación nos indica que el gradiente es ortogonal al vector infinitesimal dr y donde este vector pertenece al plano que es tangente a la superficie j (x, y, z) = c. en el punto (x, y, z).

Y otra última observación. Para denotar la derivada direccional de un campo escalar en la dirección de un vector unitario u, utilizaremos algunas veces la expresión (del miembro izquierdo)

Derivada direccional y gradiente de un campo escalar