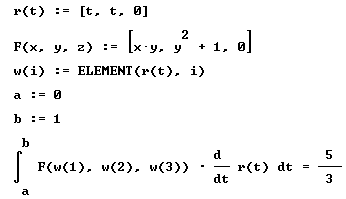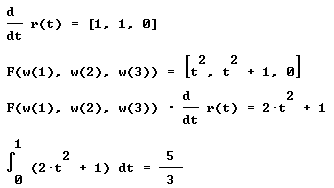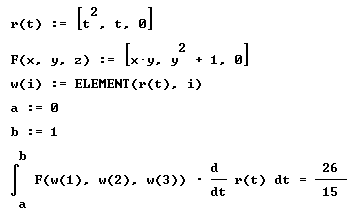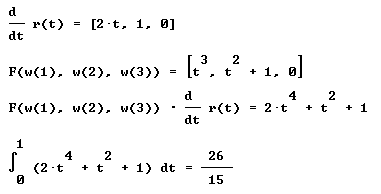| Daremos dos ejemplos para calcular una integral de línea
para dos caminos diferentes que conectan los mismos puntos.
|
| Para el campo vectorial F( x, y, z ) = xy
i + ( y2 + 1 ) j + 0 k
queremos calcular la integarl
|
|
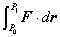
|
| donde P0 = (0, 0, 0) y P1
= (1, 1, 0), y la curva C es:
|
| ( i ) la línea recta que une los puntos P0
y P1;
|
| ( ii ) la curva dada por y2 = x
|
| Para el caso ( i ) el cálculo de la integral sigue la
siguiente secuencia:
|
|
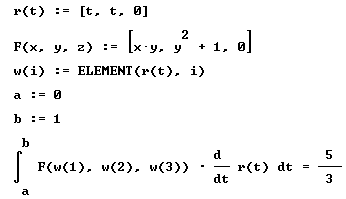
|
| En efecto, puesto que
|
|
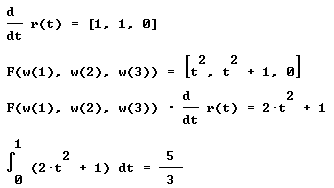
|
| Para el caso ( ii ), se puede ver que una conveniente
parametrización de la curva es r( t ) = t2
i + t j + 0 k, de modo que el cálculo de la
integral sigue la secuencia:
|
|
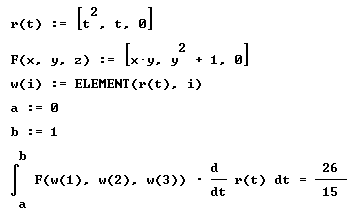
|
| En efecto, puesto que los cálculos involucrados son
|
|
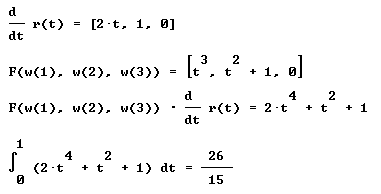
|
| Y podemos observar que ambos resultados son distintos,
conforme a que los caminos fueron distintos para la conexión de los
mismos puntos.
|