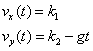Anterior

Avanzar

Principal

Aplicaciones y ejemplos

Ejemplo 1. La posición de una partícula se describe por el siguiente vector r = t2 i + ln t j + e2t k. Encontrar la velocidad y la aceleración de esta partícula. 
Por lo que hemos visto en la sección anterior, la velocidad y la aceleración se obtienen por derivación. En efecto, derivando el vector posición obtenemos la velocidad

Y nuevamente derivamos para obtener la aceleración

CUIDADO: Este ejemplo es absolutamente absurdo e irreal, NO EXISTE partícula que tenga esta función de posición extremadamente violenta (considere el tiempo medido en segundos, y entregue un razonamiento de que no existe tal partícula)
Ejemplo 2. Una partícula se mueve alrededor de un círculo de radio a, como lo indica la Figura 1, y esta partícula lleva una velocidad angular constante w. Encontrar la velocidad y la aceleración. 
Este tipo de movimiento se llama movimiento circular uniforme. Sin pérdida de generalidad, podemos suponer que en el tiempo t = 0 la partícula se encuentra en la posición cartesiana (a, 0), de esta forma el ángulo, como variable que es, está determinado por la expresión

q = w t
Además, las coordenadas cartesianas de la posición de la partícula están dadas por

 

 

 

 

Figura 1

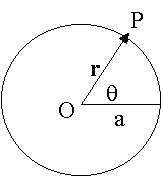
de modo que el vector posición  de la partícula está dado por

r = i a cos wt + j a sen wt
Podemos notar que la magnitud de r es constante y vale a (solo la dirección varía). Derivando tenemos que

v = - i aw sen wt + j aw cos wt

a = - i aw2 cos wt - j aw2 sen wt = -w2 r
 estas expresiones podemos concluir que el vector velocidad es tangente a la tayectoria toda vez que es perpendicular al vector posición, en efecto

r . v = - a2w sen wt cos wt + a2w sen wt cos wt = 0
Además la aceleración es de magnitud constante, aw2, y su dirección es opuesta a la dirección radial. Esta aceleración es la llamada aceleración centrípeta.
Aplicación. La segunda ley de Newton. Esta ley establece que la razón de cambio del momentum (cantidad de movimiento) de un cuerpo es igual a la resultante de las fuerzas externas que se aplican sobre el cuerpo, de otra forma

donde m es la masa y F es la fuerza resultante externa. Si F = F1 i + F2 j + F3 k entonces

siendo r = x( t ) i + y( t ) j + z( t ) k.
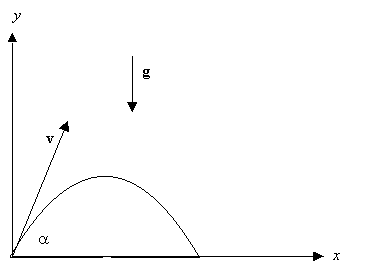
Ejemplo 3. Un proyectil es lanzado con una velocidad V y un ángulo a respecto de la horizontal. Si la resistencia del aire es despreciable y la única fuerza externa es debido a la gravedad (que se supone constante). Discuta este movimiento.
Ajustemos los ejes ortogonales haciendo coincidir el origen con la posición de salida del proyectil, siendo x el eje horizontal e y el eje vertical, conforme lo indica la Figura 2.
En este caso la masa m es constante, y la única fuerza externa que actúa es F = m g, donde g = - g j, es la aceleración de gravedad o gravitacional. Bajo estas circunstancias tenemos la ecuación diferencial

que en sus componentes es equivalente al sistema

siendo v = vx i + vy j.

Figura 2
Resolviendo las ecuaciones diferenciales anteriores, tenemos que

Vectorialmente nos queda

donde el vector constante A se determina por la condición inicial de que en el tiempo t = 0, se tiene que

v( 0 ) = A = i V cos a + j V sen a
De tal forma que

v( t ) = i V cos a + j (V sen a - g t)
Ahora resolviendo la ecuación diferencial vectorial

con condición inicial r( 0 ) = 0, obtenemos

r( t ) = i V t cos a + j (V t sen a - (1/2)g t2 )
Las ecuaciones paramétricas de la trayectoria son

x( t ) = V t cos a ;    y( t ) = V t sen a - (1/2)g t2               (1)
El intervalo de "vuelo" del proyectil está dada por la ecuación y ( t ) = 0 cuyas soluciones son 

t = 0 ;  t = 2 V sen a / g
En el tiempo t = 0 el proyectil sale, y en el tiempo t = T = 2 V sen a / g el proyectil cae al suelo, y en este tiempo T la distancia horizontal recorrida, llamada Rango, es R = x( T ) = 2V2 sen a cos a / g = V2 sen 2a / g.
Si la velocidad de salida V es constante, entonces R solo depende de a, y este rango será máximo cuando a = p / 4.
En las ecuaciones dadas en (1) reemplazamos el valor de t, y obtenemos

ecuación que nos indica que la trayectoria del proyectil es una parábola.
Ejemplo 4. Encontrar las ecuaciones que modelan el movimiento de un cohete de masa m, velocidad v( t ), y velocidad de combustión c, y no hay fuerzas externas sobre el cohete.
Puesto que no hay fuerzas externas actuando sobre el sistema, el momentum o cantidad de movimiento debe ser constante. Supongamos que en el tiempo t la más del cohete más la masa del combustible es m( t ) con una velocidad v( t ); mientras que en el tiempo t + Dt la masa del cohete es m( t + Dt ) y lleva una velocidad de v(t + Dt), y la masa del combustible expelido es m( t ) - m( t + Dt ), y esta masa de gas sale con una velocidad de v(t + Dt) - c. En virtud de que la cantidad de movimiento se conserva, tenemos que

m( t + Dt ) v(t + Dt) + [m( t ) - m( t + Dt )] (v(t + Dt) - c) = m( t ) v( t )
Trabando algebraicamente, tenemos  que

m( t + Dt ) v(t + Dt) + m( t ) v(t + Dt) - m( t + Dt ) v(t + Dt) - m( t ) c + m( t + Dt ) c = m( t ) v( t )
nos queda

m( t ) v(t + Dt) + c (m( t + Dt ) - m( t )) = m( t ) v( t )

m( t ) v(t + Dt) - m( t ) v( t ) = - c (m( t + Dt ) - m( t ))
dividiendo por Dt esta igualdad, y pasando al límite cuando Dt tiende a cero, nos queda la ecuación diferencial vectorial

la integral vectorial de esta ecuación diferencial es (sino lo sabe hacer haga click aquí)

Suponga que un cohete tiene una velocidad de combustión de magnitud , y las 3/4 partes del cohete, al inicio, corresponde a masa de combustible. ¿Qué rapidez tendrá el cohete en el instante mismo que consuma todo el combustible (tiempo de quemado)?
Como el cohete funciona solo a "propulsión a  chorro" entonces v( 0 ) = 0, y si la masa del cohete es, digamos, M, entonces en el "tiempo de quemado" la masa del cohete será de M / 4. Luego, si llamamos t0 el tiempo de quemado entonces

v( t0 ) =  c ln [m( t0 ) / m( 0 )] = c ln 1 / 4
en consecuencia, la rapidez será