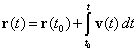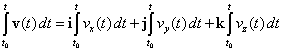Diferenciación de funciones vectoriales de una sola variable

En muchos casos de interés los vectores no son constantes, sino más bien dependen de uno o más escalares. En esta sección estudiaremos funciones vectoriales de una sola variable, y, salvo que se indique lo contrario, esta variable estará asociada al tiempo.

Supongamos que una cierta partícula (un molécula, el centro de masa de un objeto no muy grande, incluso hasta un satélite) tiene una determinada posición en el espacio (en coordenadas rectangulares de orientación positiva) en función del tiempo, de otra forma está partícula (generalmente) se está moviendo. Las coordenadas de esta partícula, entonces, en un determinado instante t están dadas por

x = x ( t ) ; y = y ( t ) ; z = z ( t ) (1)

Las ecuaciones en (1) son llamadas ecuaciones paramétricas de la trayectoria en términos del parámetro tiempo. Y esto significa que para cualquier tiempo t, podemos localizar la posición (x, y, z) de la partícula. Una manera adecuada para describir el movimiento de esta partícula es mediante el vector posición, esto es

r = r( t ) = x( t ) i + y( t ) j + z( t ) k (2)

Dado que el vector posición r( t ) es conocido, ¿cómo podemos calcular la velocidad de la partícula? La solución es muy sencilla.

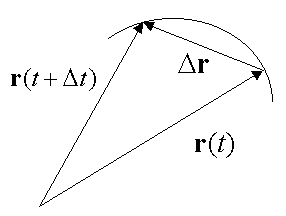
En el tiempo t + Dt la posición del vector será r( t + Dt ), esto es

r( t + Dt) = x( t + Dt ) i + y( t + Dt ) j + z( t + Dt ) k (3)

de manera que el desplazamiento (el vector desplazamiento) en el intervalo de tiempo [t, t + Dt] está dado por

r( t + Dt) - r( t ) (4)

El vector dado en (4), con abuso de notación, se denota por Dr, es decir Dr = r( t + Dt) - r( t ). Este vector se puede observar en la Figura 1.

Para un intervalo de tiempo Dt muy pequeño el desplazamiento Dr se aproximará a la tangente de la curva de la trayectoria, en el punto x( t ), y( t ), z( t ), como se puede observar en la Figura 1.

Luego, la velocidad media de la partícula en el intervalo de tiempo [t, t + Dt] está dado por

La velocidad instantánea v es simplemente el límite de la velocidad media cuando Dt tiende a cero, es decir

(4)

Figura 1

El cálculo de esta velocidad descansa en las componentes del vector posición. En efecto, puesto que

entonces, pasando al límite las componentes, tenemos que

(5)

y las cantidades (si es que existen) dx/dt, dy/dt, dz/dt son las velocidades componentes.

La aceleración se encuentra de la misma manera, esto es a = dv/dt = d²r/dt² es

De tal forma que la diferenciación de funciones vectoriales de una sola variable es sencilla, y se desarrolla aplicando las reglas de diferenciación a las funciones escalares que constituyen las componentes de la función vectorial. Con un razonamiento análogo, podemos determinar la integración de este tipo de funciones, puesto que es el proceso inverso a la derivación. Por ejemplo, si conocemos la función v( t ) = v_x( t ) i + v_y( t ) j + v_z( t ) k, entonces la solución de la ecuación diferencial vectorial

está dada por

siendo